Difference between revisions of "Manuals/calci/COMPLEMENT"
(Created page with "complement") |
|||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | complement | + | <div style="font-size:30px">'''COMPLEMENT (B,A) '''</div><br/> |
| + | *<math>B</math> and <math>A</math> are any two sets. | ||
| + | |||
| + | ==Description== | ||
| + | *This function shows the complement of the given sets. | ||
| + | *In <math>COMPLEMENT (B,A)</math>, <math>B</math> and <math>A</math> are two sets. | ||
| + | *In Set theory,the complement of a set A refers to elements not in A and which will be in the set B(Universal set). | ||
| + | *So complement os A is defined by:The relative complement of A with respect to a set B, also termed the difference of sets A and B, written <math>\frac{B}{A}</math>, is the set of elements in B but not in A. | ||
| + | *When all sets under consideration are considered to be subsets of a given set U(Universal Set), the absolute complement of A is the set of elements in U but not in A. | ||
| + | |||
| + | ==Examples== | ||
| + | #COMPLEMENT([19,14,17,23,45,89],[89,90,14,45,32,10,1]) = 90 32 10 1 | ||
| + | #COMPLEMENT([1,2,3,4,5,6,7,8,9,10],[8,9,10,11,12,13,14,15,16]) = 11 12 13 14 15 16 | ||
| + | #COMPLEMENT([67,12,20,56,10,18],[67,12,20,56]) = Null | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=2B4EBvVvf9w|280|center|Complement}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| + | *[[Manuals/calci/COMPLEXNUM | COMPLEXNUM ]] | ||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
| + | |||
| + | ==References== | ||
| + | [https://en.wikipedia.org/wiki/Complement_(set_theory) Complement] | ||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 14:17, 11 December 2018
COMPLEMENT (B,A)
- and are any two sets.
Description
- This function shows the complement of the given sets.
- In , and are two sets.
- In Set theory,the complement of a set A refers to elements not in A and which will be in the set B(Universal set).
- So complement os A is defined by:The relative complement of A with respect to a set B, also termed the difference of sets A and B, written , is the set of elements in B but not in A.
- When all sets under consideration are considered to be subsets of a given set U(Universal Set), the absolute complement of A is the set of elements in U but not in A.
Examples
- COMPLEMENT([19,14,17,23,45,89],[89,90,14,45,32,10,1]) = 90 32 10 1
- COMPLEMENT([1,2,3,4,5,6,7,8,9,10],[8,9,10,11,12,13,14,15,16]) = 11 12 13 14 15 16
- COMPLEMENT([67,12,20,56,10,18],[67,12,20,56]) = Null
 and
and 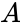 are any two sets.
are any two sets.