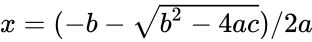Difference between revisions of "Manuals/calci/QUADRATIC"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''QUADRATIC(a,b,c)'''</div><br/> *<math>a</math>,<math>b</math> and <math>c</math> are any real numbers. ==Description== *This function gives t...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''QUADRATIC(a,b,c)'''</div><br/> | <div style="font-size:30px">'''QUADRATIC(a,b,c)'''</div><br/> | ||
*<math>a</math>,<math>b</math> and <math>c</math> are any real numbers. | *<math>a</math>,<math>b</math> and <math>c</math> are any real numbers. | ||
| + | **QUADRATIC(),returns the quadratic equation | ||
| − | |||
==Description== | ==Description== | ||
*This function gives the root values of a quadratic equation. | *This function gives the root values of a quadratic equation. | ||
| − | *In | + | *In elementary algebra, general quadratic equation is <math>a{x^2}+bx+c</math> where <math>a</math>,<math>b</math> and <math>c</math> are constant values and <math>x</math> is unknown. |
*Constant <math>a</math> cannot be equal to zero(0). | *Constant <math>a</math> cannot be equal to zero(0). | ||
*The roots of a quadratic equation can be calculated as - | *The roots of a quadratic equation can be calculated as - | ||
Latest revision as of 13:29, 23 October 2018
QUADRATIC(a,b,c)
- , and are any real numbers.
- QUADRATIC(),returns the quadratic equation
Description
- This function gives the root values of a quadratic equation.
- In elementary algebra, general quadratic equation is where , and are constant values and is unknown.
- Constant cannot be equal to zero(0).
- The roots of a quadratic equation can be calculated as -
and
- Geometrically, these roots represent the x values at which any parabola, explicitly given as y = ax2 + bx + c, crosses the x-axis.
- The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x^2).
It is also called an "Equation of Degree 2" (because of the "2" on the x)
- Discriminant:
(b^2 − 4ac) in the formula above is called the Discriminant, because it can "discriminate" between the possible types of answer:
when (b^2 − 4ac) is positive, we get two Real solutions
when it is zero, we get just ONE real solution (both answers are the same)
when it is negative, we get two Complex solutions.
Examples
- =QUADRATIC(5,6,1)=-1 ; -0.2
- =QUADRATIC(5,2,1)=-0.2-ⅈ0.4 ; -0.2+ⅈ0.4
- =QUADRATIC(2,3,4)= -0.75-ⅈ1.1989578808281798 ; -0.75+ⅈ1.1989578808281798
Related Videos
See Also
References
 ,
, and
and 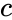 are any real numbers.
are any real numbers.
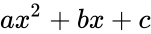 where
where  is unknown.
is unknown.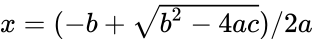 and
and