Difference between revisions of "Bartlett'sTest"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:25px">'''BARTLETTSTEST(DataRange,ConfidenceLevel,NewTableFlag)'''</div><br/> *<math>DataRange</math> is the array of x values. *<math>ConfidenceLevel</ma...") |
|||
| (50 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size:25px">'''BARTLETTSTEST(DataRange,ConfidenceLevel,NewTableFlag)'''</div | + | <div style="font-size:25px">'''BARTLETTSTEST(DataRange, ConfidenceLevel, NewTableFlag)'''</div> |
| − | *<math>DataRange</math> is the array of x values. | + | *'''<math>DataRange</math> is the array of x values. |
| − | *<math>ConfidenceLevel</math> is the value from 0 to 1. | + | *'''<math>ConfidenceLevel</math> is the value from 0 to 1. |
| − | *<math>NewTableFlag</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube. | + | *'''<math>NewTableFlag</math> is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.<br></br> |
| − | == | + | ==='''DESCRIPTION=== |
| − | * Bartlett's test is used to test if k samples are from populations with equal variances. | + | * '''Bartlett's test is used to test if k samples are from populations with equal variances. |
| − | * Bartlett's test is sensitive to departures from normality. | + | * '''Bartlett's test is sensitive to departures from normality. |
| − | * That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality. | + | * '''That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality. |
| − | <math>B=\frac{df_WlnMS_W-\ | + | <math>B=\frac{df_WlnMS_W-\sum_{j}df_jln s_j^2}{1+\frac{1}{3(k-1)}(\sum_{j}\frac{1}{df_j}-\frac{1}{df_W})}</math> |
| + | * '''B is the Bartlett's test static. | ||
| + | * '''<math>MS_W</math> is the pooled variance across all groups.<br></br> | ||
| + | |||
| + | ==='''RESULT=== | ||
| + | * '''If p-value is greater than BCritical value, reject the null hypothesis. | ||
| + | * '''Else, retain null hypothesis.<br></br> | ||
| + | |||
| + | ==='''EXAMPLE=== | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !!C !!D | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 51 || 82 || 79 || 85 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 87 || 91 || 84 || 80 | ||
| + | |- | ||
| + | !3 | ||
| + | | 50 || 92 || 74 || 65 | ||
| + | |- | ||
| + | !4 | ||
| + | | 48 || 80 || 98 || 71 | ||
| + | |- | ||
| + | !5 | ||
| + | | 79 || 52 || 63 || 67 | ||
| + | |- | ||
| + | !6 | ||
| + | | 61 || 79 || 83 || 51 | ||
| + | |- | ||
| + | !7 | ||
| + | | 53 || 73 || 85 || 63 | ||
| + | |- | ||
| + | !8 | ||
| + | |54 || 74 || 58 || 93 | ||
| + | |} | ||
| + | ='''BARTLETTSTEST([A1:A8, B1:B8, C1:C8, D1:D8], 0.05, true)<br></br> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+BARTLETT'S TEST | ||
| + | |- | ||
| + | ! !!DATA-0!!DATA-1!! DATA-2!!DATA-3 | ||
| + | |- | ||
| + | |MEAN||60.375||77.875||78||71.875 | ||
| + | |- | ||
| + | |VARIANCE || 214.26785714285714 || 157.55357142857142 || 164.57142857142858 || 181.55357142857142 | ||
| + | |- | ||
| + | |LNVARIANCE || 5.367226901229239 || 5.059765536486956 || 5.1033446922005234 || 5.201550769540011 | ||
| + | |- | ||
| + | |COUNT || 8 || 8 || 8 || 8 | ||
| + | |- | ||
| + | |DF || 7 || 7 || 7 || 7 | ||
| + | |- | ||
| + | |1/DF || 0.14285714285714285 || 0.14285714285714285 || 0.14285714285714285 || 0.14285714285714285 | ||
| + | |} | ||
| + | {| class="wikitable" | ||
| + | |+ERROR | ||
| + | |- | ||
| + | ! !! SAMPLE DATA | ||
| + | |- | ||
| + | |DF || 28 | ||
| + | |- | ||
| + | | 1/DF || 0.03571428571428571 | ||
| + | |- | ||
| + | |VARIANCE || 179.48660714285714 | ||
| + | |- | ||
| + | |LNVARIANCE || 5.19010059312721 | ||
| + | |} | ||
| + | {| class="wikitable" | ||
| + | |+RESULTS | ||
| + | |- | ||
| + | ! !! DATA | ||
| + | |- | ||
| + | |B-NUMERATOR || 0.19960131136474502 | ||
| + | |- | ||
| + | |B-DENOMINATOR || 1.0595238095238095 | ||
| + | |- | ||
| + | |B || 0.18838775454650092 | ||
| + | |- | ||
| + | |P-VALUE || 0.979441777737987 | ||
| + | |- | ||
| + | |B-CRITICAL || 7.814684159999997 | ||
| + | |- | ||
| + | |RESULT || THE P-VALUE IS LESSER THAN THE B-CRITICAL VALUE, SO THE VARIANCES ARE JUDGED TO BE EQUAL. | ||
| + | |} | ||
| + | <br></br> | ||
| + | |||
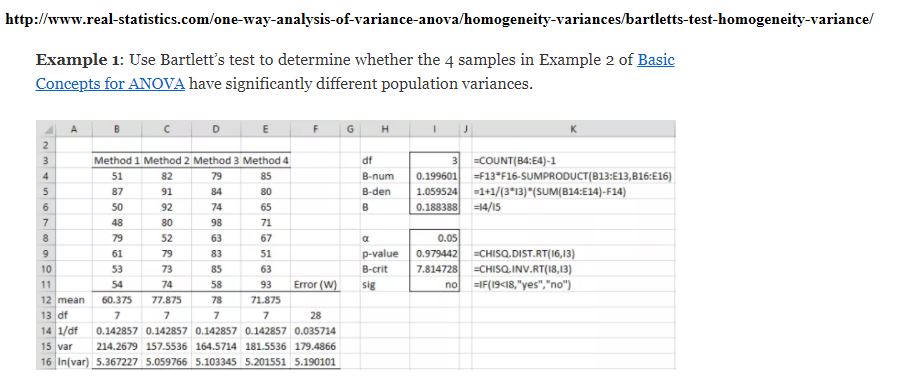
| + | ===Comparison with other software=== | ||
| + | '''Bartlett's test to determine whether the 4 samples have significantly different population variances.<br><br> | ||
| + | [[File:bart1.JPG]]<br><br> | ||
| + | |||
| + | '''SOLUTION'''<br> | ||
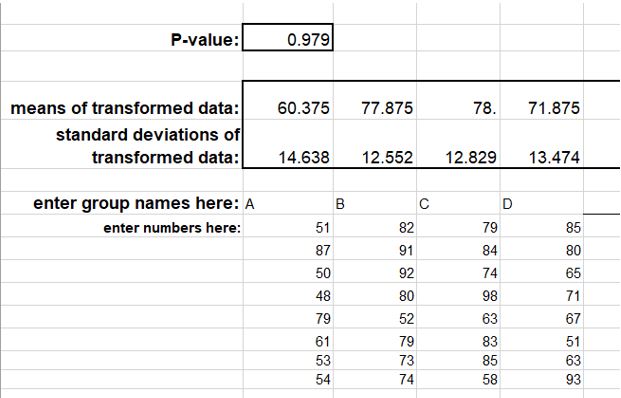
| + | '''In z3:'''<br> | ||
| + | [[File:bartz.JPG]]<br><br> | ||
| + | |||
| + | '''In R:'''<br> | ||
| + | [[File:bartr.JPG]]<br><br> | ||
| + | |||
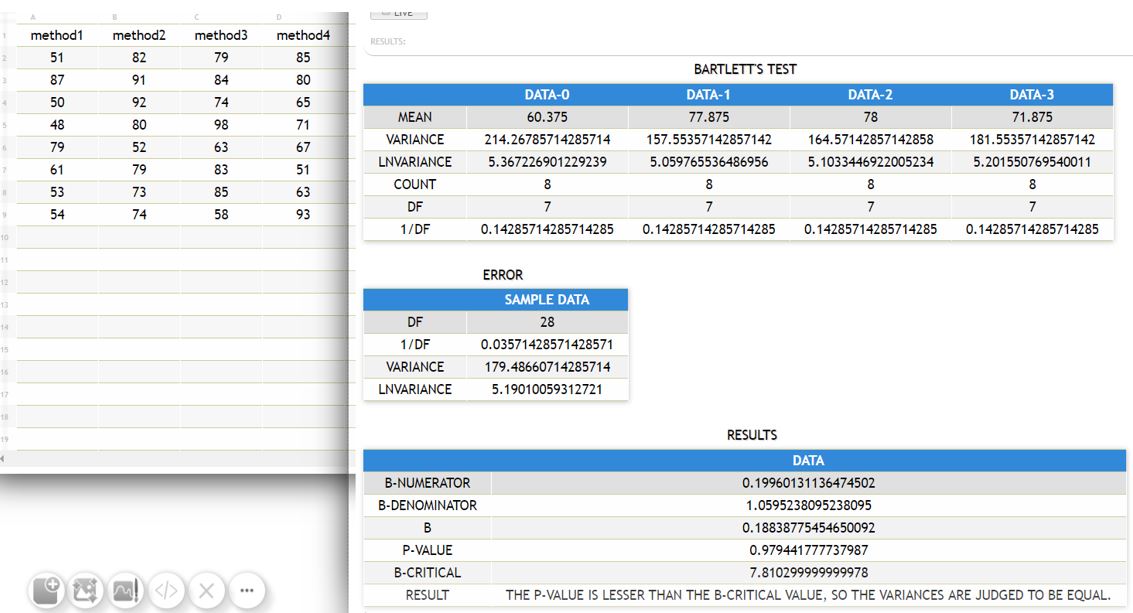
| + | '''In Online Software:'''<br> | ||
| + | [[File:bartos.JPG]]<br><br> | ||
| + | |||
| + | '''In Online Software:'''<br> | ||
| + | [[File:bartos2.JPG]]<br><br> | ||
| + | |||
| + | * z3 and the online software give the same P-value i.e 0.979. | ||
| + | * R has a P-value of 0.9768. | ||
Latest revision as of 07:31, 19 August 2020
BARTLETTSTEST(DataRange, ConfidenceLevel, NewTableFlag)
- is the array of x values.
- is the value from 0 to 1.
- is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
DESCRIPTION
- Bartlett's test is used to test if k samples are from populations with equal variances.
- Bartlett's test is sensitive to departures from normality.
- That is, if the samples come from non-normal distributions, then Bartlett's test may simply be testing for non-normality.
- B is the Bartlett's test static.
- is the pooled variance across all groups.
RESULT
- If p-value is greater than BCritical value, reject the null hypothesis.
- Else, retain null hypothesis.
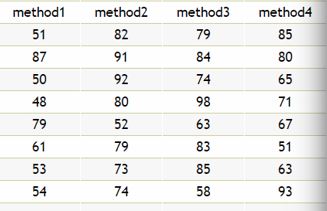
EXAMPLE
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 51 | 82 | 79 | 85 |
| 2 | 87 | 91 | 84 | 80 |
| 3 | 50 | 92 | 74 | 65 |
| 4 | 48 | 80 | 98 | 71 |
| 5 | 79 | 52 | 63 | 67 |
| 6 | 61 | 79 | 83 | 51 |
| 7 | 53 | 73 | 85 | 63 |
| 8 | 54 | 74 | 58 | 93 |
=BARTLETTSTEST([A1:A8, B1:B8, C1:C8, D1:D8], 0.05, true)
| DATA-0 | DATA-1 | DATA-2 | DATA-3 | |
|---|---|---|---|---|
| MEAN | 60.375 | 77.875 | 78 | 71.875 |
| VARIANCE | 214.26785714285714 | 157.55357142857142 | 164.57142857142858 | 181.55357142857142 |
| LNVARIANCE | 5.367226901229239 | 5.059765536486956 | 5.1033446922005234 | 5.201550769540011 |
| COUNT | 8 | 8 | 8 | 8 |
| DF | 7 | 7 | 7 | 7 |
| 1/DF | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 | 0.14285714285714285 |
| SAMPLE DATA | |
|---|---|
| DF | 28 |
| 1/DF | 0.03571428571428571 |
| VARIANCE | 179.48660714285714 |
| LNVARIANCE | 5.19010059312721 |
| DATA | |
|---|---|
| B-NUMERATOR | 0.19960131136474502 |
| B-DENOMINATOR | 1.0595238095238095 |
| B | 0.18838775454650092 |
| P-VALUE | 0.979441777737987 |
| B-CRITICAL | 7.814684159999997 |
| RESULT | THE P-VALUE IS LESSER THAN THE B-CRITICAL VALUE, SO THE VARIANCES ARE JUDGED TO BE EQUAL. |
Comparison with other software
Bartlett's test to determine whether the 4 samples have significantly different population variances.
- z3 and the online software give the same P-value i.e 0.979.
- R has a P-value of 0.9768.
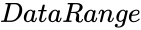 is the array of x values.
is the array of x values.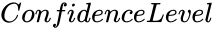 is the value from 0 to 1.
is the value from 0 to 1.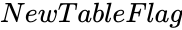 is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.
is either TRUE or FALSE. TRUE for getting results in a new cube. FALSE will display results in the same cube.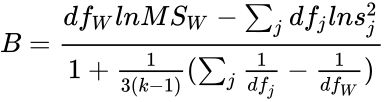
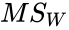 is the pooled variance across all groups.
is the pooled variance across all groups.