Difference between revisions of "Manuals/calci/MATRIXDIVPARTS"
Jump to navigation
Jump to search
| (One intermediate revision by the same user not shown) | |||
| Line 14: | Line 14: | ||
==Examples== | ==Examples== | ||
| − | + | 1. MATRIXDIVPARTS([[6,16],[10,-12]],[[4,4],[5,4]]) | |
{| border="1" cellpadding="5" cellspacing="0" | {| border="1" cellpadding="5" cellspacing="0" | ||
|- | |- | ||
| Line 27: | Line 27: | ||
-3 0 | -3 0 | ||
|} | |} | ||
| − | + | 2. MATRIXDIVPARTS([[4,5,10],[-12,34,31]],[[17,18,27],[29,-24,31]]) | |
{| border="1" cellpadding="5" cellspacing="0" | {| border="1" cellpadding="5" cellspacing="0" | ||
| Line 46: | Line 46: | ||
1 0 | 1 0 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=oTJ7R2ziR28&t=2s|280|center|Matrix Division}} | ||
Latest revision as of 13:51, 12 April 2019
MATRIXDIVPARTS (a,b)
- and are any two matrices.
Description
- This function shows the quotient and remainder of the given two matrices.
- In , and are two matrices.
- Normally we could not do the matrix division directly.
- Instead of that we can multiply by an inverse.
- This function is taking corresponding entries and doing the division for each element.
- Also it is showing the first entry as quotient and the second entry as remainder of each division.
- For example, MATRIXDIVPARTS([[6,16],[10,-12]],[[4,4],[5,4]]) in this matrices results (1,1) entry as 1 and 2.
- 1 is the quotient and 2 is the remainder of the 6/4.
- (1,2) entry as 4 and 0,4 is the quotient and 0 is the remainder of 16/4 and so on.
Examples
1. MATRIXDIVPARTS([[6,16],[10,-12]],[[4,4],[5,4]])
1 2 |
4 0 |
|
2 0 |
-3 0 |
2. MATRIXDIVPARTS([[4,5,10],[-12,34,31]],[[17,18,27],[29,-24,31]])
0 4 |
0 5 |
0 10 |
-1 17 |
-2 -14 |
1 0 |
Related Videos
 and
and  are any two matrices.
are any two matrices.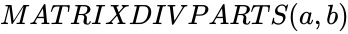 ,
,