Difference between revisions of "Manuals/calci/CHOLESKYFACTORIZATION"
Jump to navigation
Jump to search
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div style="font-size: | + | <div style="font-size:25px">'''CHOLESKYFACTORIZATION(Matrix)'''</div><br/> |
*<math>Matrix</math> is the array of numeric elements | *<math>Matrix</math> is the array of numeric elements | ||
| Line 42: | Line 42: | ||
<li>Compute <math>L_{22}</math> from </li> | <li>Compute <math>L_{22}</math> from </li> | ||
<math>A_{22}-L_{21}L_{21}^{T}</math> = <math>L_{22}L_{22}^{T}</math> | <math>A_{22}-L_{21}L_{21}^{T}</math> = <math>L_{22}L_{22}^{T}</math> | ||
| − | * | + | *This is a Cholesky Factorization of order <math>n-1</math> |
</ol> | </ol> | ||
| − | *If the matrix A is Hermitian and positive semi-definite, then it still has a decomposition of the form A = LL^T if the diagonal entries of L are allowed to be zero. | + | |
| − | *Also A can be written as LL^T for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite. | + | *If the matrix A is Hermitian and positive semi-definite, then it still has a decomposition of the form A = LL^T if the diagonal entries of L are allowed to be zero. |
| + | *Also A can be written as LL^T for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite. | ||
==Examples== | ==Examples== | ||
| − | 1 | + | {| class="wikitable" |
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! C | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 25 || 15 || -5 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 15 || 18 || 0 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | -5 || 0 || 11 | ||
| + | |} | ||
| + | =CHOLESKYFACTORIZATION(A1:C3) | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|+Result | |+Result | ||
| Line 58: | Line 74: | ||
| -1 || 1 || 3 | | -1 || 1 || 3 | ||
|} | |} | ||
| − | + | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 8 || 14 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 10 || 32 | ||
| + | |} | ||
| + | =CHOLESKYFACTORIZATION(A1:B2) | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|+Result | |+Result | ||
| Line 66: | Line 95: | ||
| 3.5355339059327373|| 4.415880433163924 | | 3.5355339059327373|| 4.415880433163924 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=gFaOa4M12KU|280|center|Cholesky Decomposition}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/ANTIDIAGONAL| ANTIDIAGONAL]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://www.seas.ucla.edu/~vandenbe/103/lectures/chol.pdf Cholesky Factorization] | ||
| + | |||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 13:56, 25 April 2019
CHOLESKYFACTORIZATION(Matrix)
- is the array of numeric elements
Description
- This function gives the value of Cholesky factorization.
- It is called Cholesky Decomposition or Cholesky Factorization.
- In , is the set of values.
- The Cholesky Factorization is only defined for symmetric or Hermitian positive definite matrices.
- Every positive definite matrix A can be factored as =
is lower triangular with positive diagonal elements is is the conjugate transpose value of
- Every Hermitian positive-definite matrix has a unique Cholesky decomposition.
- Here , is set of values to find the factorization value.
- Partition matrices in = is
Algorithm
- Determine and = =
- Compute from =
- This is a Cholesky Factorization of order
*If the matrix A is Hermitian and positive semi-definite, then it still has a decomposition of the form A = LL^T if the diagonal entries of L are allowed to be zero. *Also A can be written as LL^T for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite.
Examples
| A | B | C | |
|---|---|---|---|
| 1 | 25 | 15 | -5 |
| 2 | 15 | 18 | 0 |
| 3 | -5 | 0 | 11 |
=CHOLESKYFACTORIZATION(A1:C3)
| 5 | 0 | 0 |
| 3 | 3 | 0 |
| -1 | 1 | 3 |
| A | B | |
|---|---|---|
| 1 | 8 | 14 |
| 2 | 10 | 32 |
=CHOLESKYFACTORIZATION(A1:B2)
| 2.8284271247461903 | 0 |
| 3.5355339059327373 | 4.415880433163924 |
Related Videos
See Also
References
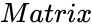 is the array of numeric elements
is the array of numeric elements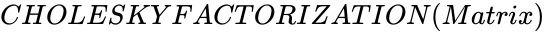 ,
, =
= 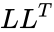
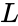 is lower triangular with positive diagonal elements
is lower triangular with positive diagonal elements
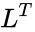 is is the conjugate transpose value of
is is the conjugate transpose value of  is set of values to find the factorization value.
is set of values to find the factorization value.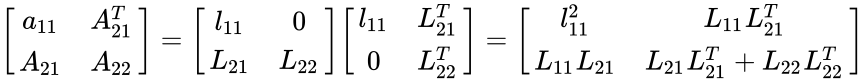
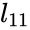 and
and 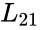

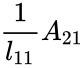
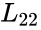 from
from  =
= 
