Difference between revisions of "Manuals/calci/POINTAT"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''POINTAT (degrees,radius,cx,cy)'''</div><br/> *<math>degrees</math> is any degree value. *<math>radius</math> is the radius value of the circle. ...") |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
*<math>Radius</math> is the radius of the circle. | *<math>Radius</math> is the radius of the circle. | ||
*Consider a circle centered at the origin with radius r, and marking the point on the circle indicated by some angle θ. | *Consider a circle centered at the origin with radius r, and marking the point on the circle indicated by some angle θ. | ||
| − | *For the point (x, y) on a circle of radius r at an angle of <math>\theta</math>,the the function <math>SIN (\theta)</math>= <math>\frac{y}{r}</math> and <math>COS(\theta)</math>=<math>\frac{x}{r}. | + | *For the point (x, y) on a circle of radius r at an angle of <math>\theta</math>,the the function <math>SIN (\theta)</math>= <math>\frac{y}{r}</math> and <math>COS(\theta)</math>=<math>\frac{x}{r}</math>. |
*Using this function we can find the coordinates of the point on the circle is <math>x= rCos(\theta)</math> and <math>y= rSin(\theta)</math>. | *Using this function we can find the coordinates of the point on the circle is <math>x= rCos(\theta)</math> and <math>y= rSin(\theta)</math>. | ||
*On a unit circle, a circle with radius 1,<math>x=Cos(\theta)</math> and <math>y=Sin(\theta)</math>. | *On a unit circle, a circle with radius 1,<math>x=Cos(\theta)</math> and <math>y=Sin(\theta)</math>. | ||
==Examples== | ==Examples== | ||
| + | 1. POINTAT(345,5) | ||
| + | {| class="wikitable" | ||
| + | |4.8296291314453415 || -1.2940952255126035 | ||
| + | |} | ||
| + | |||
| + | 2. POINTAT(280,13,2,3) | ||
| + | {| class="wikitable" | ||
| + | |4.257426309670089 || -9.802500789158707 | ||
| + | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=aHaFwnqH5CU|280|center|Point }} | ||
| + | |||
==See Also== | ==See Also== | ||
Latest revision as of 14:45, 4 March 2019
POINTAT (degrees,radius,cx,cy)
- is any degree value.
- is the radius value of the circle.
Description
- This function used to find the points on the circle using radius of the circle and degree value.
- In , is any degree value.
- is the radius of the circle.
- Consider a circle centered at the origin with radius r, and marking the point on the circle indicated by some angle θ.
- For the point (x, y) on a circle of radius r at an angle of ,the the function = and =.
- Using this function we can find the coordinates of the point on the circle is and .
- On a unit circle, a circle with radius 1, and .
Examples
1. POINTAT(345,5)
| 4.8296291314453415 | -1.2940952255126035 |
2. POINTAT(280,13,2,3)
| 4.257426309670089 | -9.802500789158707 |
Related Videos
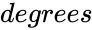 is any degree value.
is any degree value.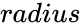 is the radius value of the circle.
is the radius value of the circle.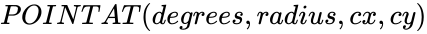 ,
,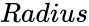 is the radius of the circle.
is the radius of the circle. ,the the function
,the the function 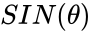 =
= 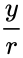 and
and 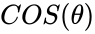 =
=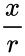 .
.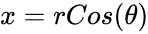 and
and 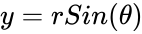 .
.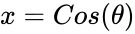 and
and 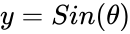 .
.