Difference between revisions of "Manuals/calci/QRDECOMPOSITION"
Jump to navigation
Jump to search
| (6 intermediate revisions by one other user not shown) | |||
| Line 26: | Line 26: | ||
|} | |} | ||
=QRDECOMPOSITION(A1:B2) | =QRDECOMPOSITION(A1:B2) | ||
| − | {| border="1" cellpadding="5" cellspacing=" | + | {| border="1" cellpadding="5" cellspacing="0" |
|- | |- | ||
| | | | ||
-0.19611613513818393 -0.9805806756909202 | -0.19611613513818393 -0.9805806756909202 | ||
| − | || -0.9805806756909202 0.19611613513818393 | + | || |
| + | -0.9805806756909202 0.19611613513818393 | ||
|- | |- | ||
| | | | ||
-10.19803902718557 13.5320133245347 | -10.19803902718557 13.5320133245347 | ||
| − | || -1.1102230246251565e-15 -8.825226081218279 | + | || |
| + | -1.1102230246251565e-15 -8.825226081218279 | ||
|} | |} | ||
| Line 56: | Line 58: | ||
| | | | ||
-0.5570860145311556 0.631547425332445 -0.5392615524675877 | -0.5570860145311556 0.631547425332445 -0.5392615524675877 | ||
| − | || -0.7427813527082074 -0.669329688618384 -0.01654176541311622 | + | || |
| − | || -0.3713906763541037 0.3913382392381005 0.841975859527614 | + | -0.7427813527082074 -0.669329688618384 -0.01654176541311622 |
| + | || | ||
| + | -0.3713906763541037 0.3913382392381005 0.841975859527614 | ||
|- | |- | ||
| − | | -5.385164807134504 -1.634118975958056 -3.528211425363985 | + | | |
| + | -5.385164807134504 -1.634118975958056 -3.528211425363985 | ||
|| | || | ||
-2.1551618871879059e-16 11.22584763714588 -9.573042563465782 | -2.1551618871879059e-16 11.22584763714588 -9.573042563465782 | ||
| − | || | + | || |
5.3446973501217775e-17 0 1.7054560140922779 | 5.3446973501217775e-17 0 1.7054560140922779 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=J41Ypt6Mftc|280|center|QR Decomposition}} | ||
| + | |||
==See Also== | ==See Also== | ||
| Line 70: | Line 80: | ||
*[[Manuals/calci/CHOLESKYFACTORIZATION| CHOLESKYFACTORIZATION]] | *[[Manuals/calci/CHOLESKYFACTORIZATION| CHOLESKYFACTORIZATION]] | ||
*[[Manuals/calci/CONFERENCE| CONFERENCE]] | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| − | |||
==References== | ==References== | ||
Latest revision as of 13:30, 2 May 2019
QRDECOMPOSITION (Matrix)
- is the set of values.
Description
- This function gives the value of QR Decomposition.
- In , is any matrix.
- QR Decomposition is also called QR Factorization.
- QR Decomposition is defined by the product of Orthogonal matrix and Upper Triangular matrix.
- Consider any square matrix A may be decomposed as , where stands for orthogonal matrix and stands for Upper Triangular matrix.
- An orthogonal matrix should satisfy , where is identity or Unitary matrix.
- is the transpose matrix of Q.
- If the given matrix A is non-singular, then this factorization is unique.
- Gram-Schmidt process is one of the process of computing decomposition in QR Decomposition method.
Examples
| A | B | |
|---|---|---|
| 1 | 2 | 6 |
| 2 | 10 | -15 |
=QRDECOMPOSITION(A1:B2)
-0.19611613513818393 -0.9805806756909202 |
-0.9805806756909202 0.19611613513818393 |
-10.19803902718557 13.5320133245347 |
-1.1102230246251565e-15 -8.825226081218279 |
| A | B | C | |
|---|---|---|---|
| 1 | 3 | 8 | -5 |
| 2 | 4 | -6.3 | 9 |
| 3 | 2 | 5 | -1 |
=QRDECOMPOSITION(A1:C3)
-0.5570860145311556 0.631547425332445 -0.5392615524675877 |
-0.7427813527082074 -0.669329688618384 -0.01654176541311622 |
-0.3713906763541037 0.3913382392381005 0.841975859527614 |
-5.385164807134504 -1.634118975958056 -3.528211425363985 |
-2.1551618871879059e-16 11.22584763714588 -9.573042563465782 |
5.3446973501217775e-17 0 1.7054560140922779 |
Related Videos
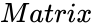 is the set of values.
is the set of values. ,
, 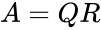 , where
, where  stands for orthogonal matrix and
stands for orthogonal matrix and 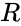 stands for Upper Triangular matrix.
stands for Upper Triangular matrix.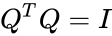 , where
, where 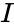 is identity or Unitary matrix.
is identity or Unitary matrix.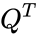 is the transpose matrix of Q.
is the transpose matrix of Q.