Difference between revisions of "Manuals/calci/DISCRETEDISTRIBUTED"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''DISCRETEDISTRIBUTED (Numbers,Values,Probability) '''</div><br/> *<math>Thing</math> is any value to test. ==Description== *This function shows ...") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''DISCRETEDISTRIBUTED (Numbers,Values,Probability) '''</div><br/> | <div style="font-size:30px">'''DISCRETEDISTRIBUTED (Numbers,Values,Probability) '''</div><br/> | ||
| − | *<math> | + | *<math>Numbers</math> is the number of variables. |
| + | *<math>Values</math> is any real number. | ||
| + | *<math>Probability</math> is the value from 0 to 1. | ||
==Description== | ==Description== | ||
| Line 9: | Line 11: | ||
*Discrete distribution is frequently used in statistical modeling and computer programming. | *Discrete distribution is frequently used in statistical modeling and computer programming. | ||
*The discrete uniform distribution itself is inherently non-parametric. | *The discrete uniform distribution itself is inherently non-parametric. | ||
| − | *Consider an interval <math>[a,b]</math>, with these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any <math>k | + | *Consider an interval <math>[a,b]</math>, with these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any <math>k \isin [a,b]</math>, as <math>F(k;a,b)=\frac{k-a+1}{b-a+1}</math>. |
*This function will return the result as error when | *This function will return the result as error when | ||
1.Any one of the parameter is non numeric. | 1.Any one of the parameter is non numeric. | ||
2.The value of a and b is<0. | 2.The value of a and b is<0. | ||
| + | |||
| + | ==Examples== | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=mrCxwEZ_22o|280|center|Discrete Distribution}} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/BERNOULLIDISTRIBUTED | BERNOULLIDISTRIBUTED ]] | ||
| + | *[[Manuals/calci/BINOMIALDISTRIBUTED | BINOMIALDISTRIBUTED ]] | ||
| + | *[[Manuals/calci/NORMALDISTRIBUTED | NORMALDISTRIBUTED ]] | ||
| + | |||
| + | ==References== | ||
| + | *[http://www.investopedia.com/terms/d/discrete-distribution.asp Discrete Distribution] | ||
| + | |||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Latest revision as of 17:10, 5 December 2018
DISCRETEDISTRIBUTED (Numbers,Values,Probability)
- is the number of variables.
- is any real number.
- is the value from 0 to 1.
Description
- This function shows the value of Discrete distribution.
- The Discrete Uniform distribution is a symmetric probability distribution whereby a finite number of values are equally likely to be distributed.
- So every one of n values has equal probability 1/n.
- Unlike a continuous distribution which has an infinite number of outcomes,a discrete distribution is characterized by a limited number of possible observations.
- Discrete distribution is frequently used in statistical modeling and computer programming.
- The discrete uniform distribution itself is inherently non-parametric.
- Consider an interval , with these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any , as .
- This function will return the result as error when
1.Any one of the parameter is non numeric. 2.The value of a and b is<0.
Examples
Related Videos
See Also
References
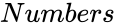 is the number of variables.
is the number of variables. is any real number.
is any real number.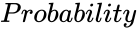 is the value from 0 to 1.
is the value from 0 to 1.![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/png/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) , with these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any
, with these conventions, the cumulative distribution function (CDF) of the discrete uniform distribution can be expressed, for any ![{\displaystyle k\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/png/a3fe7af2cc4dc30700026ed0c964382aeea60616) , as
, as 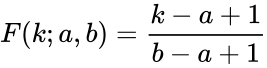 .
.