Difference between revisions of "Manuals/calci/QUATERNION"
| (6 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
*The imaginary units are satisfy certain conditions: | *The imaginary units are satisfy certain conditions: | ||
* <math>i^{2}=j^2=k^2=ijk= -1</math>. | * <math>i^{2}=j^2=k^2=ijk= -1</math>. | ||
| − | *<math>i\sdot j </math> =<math>k</math>= <math> | + | *<math>i\sdot j </math> =<math>k</math> = <math> -j \sdot i </math> |
| + | *<math>j\sdot k </math> =<math>i</math> =<math> -k\sdot j </math> | ||
| + | *<math>k\sdot i </math> =<math>j</math> = <math> -i\sdot k </math> | ||
==Examples== | ==Examples== | ||
| Line 14: | Line 16: | ||
#QUATERNION(8,-2,4,-5) = 8 -2 4 -5 | #QUATERNION(8,-2,4,-5) = 8 -2 4 -5 | ||
#QUATERNION(-9,-12,-16,-20) = -9 -12 -16 -20 | #QUATERNION(-9,-12,-16,-20) = -9 -12 -16 -20 | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=ln3vI4JEArc|280|center|Quaternion}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 16:06, 30 November 2018
QUATERNION (a,b,c,d)
- and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} are any real numbers.
Description
- This function shows the coefficient of the Quarternion.
- In Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle QUATERNION (a,b,c,d)} ,Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b,c } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} are any real numbers.
- Quartenion is a complex number of the form w + xi + yj + zk, where w, x, y, z are real numbers and i, j, k are imaginary units.
- The imaginary units are satisfy certain conditions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i^{2}=j^2=k^2=ijk= -1} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\sdot j } =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -j \sdot i }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j\sdot k } =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -k\sdot j }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\sdot i } =Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} = Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -i\sdot k }
Examples
- QUATERNION(9,2,3,4) = 9 2 3 4
- QUATERNION(8,-2,4,-5) = 8 -2 4 -5
- QUATERNION(-9,-12,-16,-20) = -9 -12 -16 -20
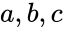 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
are any real numbers.
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d}
are any real numbers.