Difference between revisions of "Manuals/calci/MATRIX"
Jump to navigation
Jump to search
| Line 128: | Line 128: | ||
|1 || 5 || 15 || 35 || 70 | |1 || 5 || 15 || 35 || 70 | ||
|} | |} | ||
| + | |||
| + | ==Related Videos== | ||
| + | |||
| + | {{#ev:youtube|v=4lAyqscuTc8|280|center|Types of Matrices}} | ||
==See Also== | ==See Also== | ||
Latest revision as of 13:08, 9 April 2019
MATRIX (TypeOfMatrix,DimensionsOfMatrix,SeedValuesToUse,IJFunction,PreParameter,IsItInternalCall)
- is the type of the matrix.
- is the order of the matrix.
- is the range of the values to display in matrix.
Description
- This function used to give different types matrix of given order.
- Matrix is an Array of numbers which arranged in rows and columns.
- There are many types of matrices.
- So we can get a desired matrix with the given order.
- Some different types of Matrices are listed below:
- ANTIDIAGONAL
- HADAMARD
- HANKEL
- POSITIVE
- NEGATIVE
- ZERO
- POSITIVE INTEGER
- NEGATIVE INTEGER
- INTEGER
- LOGICAL
- BINARY
- BOOLEAN
- RELATION
- (0,1)
- ARROWHEAD
- ANTI SYMMETRIC
- SKEW SYMMETRIC
- BLOCK DIAGONAL
- CENTRO SYMMETRIC
- CONFERENCE
- CIRCULANT
- DIAGONAL
- FROBENIUS
- HERMITIAN
- HESSENBERG
- HILBERT
- HOLLOW INTEGER
- HOLLOW NEGZEROPOS
- HOLLOW NEGATIVE
- IDENTITY
- EXCHANGE
- LEHMER
- MONOMIAL
- GENERALIZED PERMUTATION
- METZLER
- METZLER NEGZEROPOS
- MOORE
- ALTERNANT
- ONES
- REDHEFFER
- PASCAL
- PERMUTATION
- PERSYMMETRIC
- PERSYMMETRIC INTEGER
- PERSYMMETRIC BOOLEAN
- SHIFT
- SIGNATURE
- SYMMETRIC
- SYMMETRIC BOOLEAN
- SYMMETRIC INTEGER
- TOEPLITZ
- TRIANGULAR
- UPPER TRIANGULAR
- LOWER TRIANGULAR
- CAUCHY
- CIRCULANT INTEGER
- SIGN
- UPPER BIDIAGONAL
- LOWER BIDIAGONAL
- BIDIAGONAL
- PENTA DIAGONAL
- PENTA DIAGONAL NEGATIVE
- TRIDIAGONAL
- IDEMPOTENT
- VANDERMONDE
Examples
1. MATRIX("UPPERTRIANGULAR",3)
| -37 | 82 | -52 |
| 0 | -31 | 2 |
| 0 | 0 | 13 |
2. MATRIXWITH(3,"negative:integer")
| -100 | -29 | -51 |
| -80 | -26 | -58 |
| -57 | -29 | -69 |
3. MATRIX("circulant",3,12..120..13)
| 12 | 38 | 25 |
| 25 | 12 | 38 |
| 38 | 25 | 12 |
4.MATRIX("generalized permutation",4,100..110)
| 0 | 0 | 100 | 0 |
| 0 | 0 | 0 | 101 |
| 0 | 102 | 0 | 0 |
| 103 | 0 | 0 | 0 |
5.MATRIX("pascal",5)
| 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | 15 |
| 1 | 4 | 10 | 20 | 35 |
| 1 | 5 | 15 | 35 | 70 |
Related Videos
See Also
References
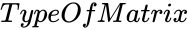 is the type of the matrix.
is the type of the matrix.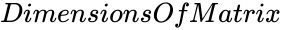 is the order of the matrix.
is the order of the matrix.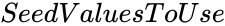 is the range of the values to display in matrix.
is the range of the values to display in matrix.