Difference between revisions of "Manuals/calci/PERFECTNUMBERS"
Jump to navigation
Jump to search
| (4 intermediate revisions by the same user not shown) | |||
| Line 18: | Line 18: | ||
==DEFICIENTNUMBERS== | ==DEFICIENTNUMBERS== | ||
| − | *Deficient number is a number <math>n</math> for which the sum of divisors <math>\sigma(n)<2n</math>, or, equivalently, the sum of proper divisors (or aliquot sum) <math>s(n)<n</math>. The value <math>2n − sigma(n)</math> (or <math>n − s(n)</math>) is called the number's deficiency. | + | *Deficient number is a number <math>n</math> for which the sum of divisors <math>\sigma(n)<2n</math>, or, equivalently, the sum of proper divisors (or aliquot sum) <math>s(n)<n</math>. The value <math>2n</math> − <math>\sigma(n)</math> (or <math>n</math> − <math>s(n)</math>) is called the number's deficiency. |
| + | *Properties of Deficient Numbers are: | ||
| + | *The aliquot sums of prime numbers equal 1, all prime numbers are deficient. | ||
| + | *An infinite number of both even and odd deficient numbers exist. | ||
| + | *All odd numbers with one or two distinct prime factors are deficient. | ||
| + | *All proper divisors of deficient or perfect numbers are deficient. | ||
| + | *Some of the Deficient numbers are: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17 and etc. | ||
| + | *DEFICIENTNUMBERS(110) = 2 3 4 5 7 8 9 10 11 13 14 15 16 17 19 21 22 23 25.......... | ||
==Examples== | ==Examples== | ||
| Line 24: | Line 31: | ||
#PERFECTNUMBERS(900,54) = 6 28 496 | #PERFECTNUMBERS(900,54) = 6 28 496 | ||
#PERFECTNUMBERS(-567,0) = NaN | #PERFECTNUMBERS(-567,0) = NaN | ||
| + | #PERFECTNUMBERS(10) = 6 | ||
==Related Videos== | ==Related Videos== | ||
Latest revision as of 03:14, 11 February 2020
PERFECTNUMBERS (Upto,StartFrom)
- is the maximum number limit.
- is the minimum number limit.
Description
- This function returns the list of Perfect numbers.
- In PERFECTNUMBERS (Upto,StartFrom),Upto is the Maximum number limit to display and Start from is the Minimum number to start Perfect number list.
- Perfect number is a positive integer which is equal to the sum of its proper divisors.
- The smallest perfect number is 6, which is the sum of 1, 2, and 3.
ABUNDANTNUMBERS
- Abundant number is a number for which the sum of its proper divisors is greater than the number itself.
- It is also called Excessive Number.
- The first Abundant number is 12.
- Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16.
- The amount by which the sum exceeds the number is the abundance. The number 12 has an abundance of 4.
- ABUNDANTNUMBERS(110) = 12 18 20 24 30 36 40 42 48 54 56 60 66 70 72 78 80 84 88 90 96 100 102 104 108
DEFICIENTNUMBERS
- Deficient number is a number for which the sum of divisors , or, equivalently, the sum of proper divisors (or aliquot sum) . The value − (or − ) is called the number's deficiency.
- Properties of Deficient Numbers are:
- The aliquot sums of prime numbers equal 1, all prime numbers are deficient.
- An infinite number of both even and odd deficient numbers exist.
- All odd numbers with one or two distinct prime factors are deficient.
- All proper divisors of deficient or perfect numbers are deficient.
- Some of the Deficient numbers are: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17 and etc.
- DEFICIENTNUMBERS(110) = 2 3 4 5 7 8 9 10 11 13 14 15 16 17 19 21 22 23 25..........
Examples
- PERFECTNUMBERS(14,2) = 6
- PERFECTNUMBERS(900,54) = 6 28 496
- PERFECTNUMBERS(-567,0) = NaN
- PERFECTNUMBERS(10) = 6
Related Videos
See Also
References
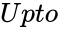 is the maximum number limit.
is the maximum number limit.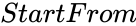 is the minimum number limit.
is the minimum number limit. for which the sum of divisors
for which the sum of divisors 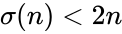 , or, equivalently, the sum of proper divisors (or aliquot sum)
, or, equivalently, the sum of proper divisors (or aliquot sum) 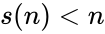 . The value
. The value 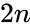 −
− 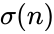 (or
(or 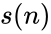 ) is called the number's deficiency.
) is called the number's deficiency.