Difference between revisions of "Manuals/calci/IMEXP"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMEXP(ComplexNumber)'''</div><br/> |
| + | *<math>ComplexNumber</math> is of the form x+iy. | ||
| + | **IMEXP(), returns the exponential of a complex number. | ||
| − | |||
| − | + | ==Description== | |
| − | |||
| − | |||
| − | + | *This function gives the exponential of a complex number. | |
| + | *In <math>IMEXP(ComplexNumber)</math>, <math>ComplexNumber</math> is of the form <math>x+iy</math>, <math>x</math>&<math>y</math> are real numbers & <math>i</math> is the imaginary unit. <math>i=\sqrt{-1}</math>. | ||
| + | *Euler's formula states that <math>e^{ix}= cosx+isinx</math>, for any real number <math>x</math> and <math>e</math> is the base of the natural logarithm. | ||
| + | *The approximate value of the constant e=2.718281828459045 and it is equal to <math>e^1</math>. | ||
| + | *Let z be the Complex Number.Then the exponential of a complex number is : <math>IMEXP(z) = e^z = e^{x+iy} = e^{x}.e^{iy} = e^{x}.(cosy+isiny)=e^x.cosy+ie^x.siny</math>. | ||
| + | *Here Sin and Cos are trignometric functions. y is angle value in radians. | ||
| + | *When imaginary part is '0', it will give the exponent value of the real number. i.e <math>IMEXP(z) = EXP(z)</math> when imaginary number <math>iy</math> is '0'. | ||
| + | *The Complex exponential function is denoted by "'''cis(x)'''"(Cosine plus iSine) | ||
| + | *We can use [[Manuals/calci/COMPLEX | COMPLEX ]] function to convert the real and imaginary coefficients to a complex number. | ||
| − | + | ==ZOS== | |
| − | |||
| − | |||
| − | + | *The syntax is to calculate IMEXP in ZOS is <math>IMEXP(ComplexNumber)</math>. | |
| + | **<math>ComplexNumber</math> is of the form a+bi. | ||
| + | *For e.g.,IMEXP("0.3-0.54i") | ||
| + | {{#ev:youtube|nuPmQ8dB3wc|280|center|IMEXP}} | ||
| − | + | ==Examples== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | #=IMEXP("2+3i") = -7.315110094901102+1.0427436562359i | |
| + | #=IMEXP("4-5i") = 15.4874305606508+52.355491418482i | ||
| + | #=IMEXP("6") = 403.428793492735+0i | ||
| + | #=IMEXP("2i") = -0.416146836547142+0.909297426825682i | ||
| + | #=IMEXP("0") = 1+0i and IMEXP("0i") = 1+0i | ||
| − | + | ==Related Videos== | |
| − | |||
| − | |||
| − | + | {{#ev:youtube|lNEoaXWkzvw|280|center|Exponential Form of Complex Number}} | |
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | |
| − | + | *[[Manuals/calci/IMAGINARY | IMAGINARY ]] | |
| − | + | *[[Manuals/calci/IMREAL | IMREAL ]] | |
| − | + | *[[Manuals/calci/EXP | EXP ]] | |
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/Exponential_function Exponential function] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 15:36, 19 July 2018
IMEXP(ComplexNumber)
- is of the form x+iy.
- IMEXP(), returns the exponential of a complex number.
Description
- This function gives the exponential of a complex number.
- In , is of the form , & are real numbers & is the imaginary unit. .
- Euler's formula states that , for any real number and is the base of the natural logarithm.
- The approximate value of the constant e=2.718281828459045 and it is equal to .
- Let z be the Complex Number.Then the exponential of a complex number is : .
- Here Sin and Cos are trignometric functions. y is angle value in radians.
- When imaginary part is '0', it will give the exponent value of the real number. i.e when imaginary number is '0'.
- The Complex exponential function is denoted by "cis(x)"(Cosine plus iSine)
- We can use COMPLEX function to convert the real and imaginary coefficients to a complex number.
ZOS
- The syntax is to calculate IMEXP in ZOS is .
- is of the form a+bi.
- For e.g.,IMEXP("0.3-0.54i")
Examples
- =IMEXP("2+3i") = -7.315110094901102+1.0427436562359i
- =IMEXP("4-5i") = 15.4874305606508+52.355491418482i
- =IMEXP("6") = 403.428793492735+0i
- =IMEXP("2i") = -0.416146836547142+0.909297426825682i
- =IMEXP("0") = 1+0i and IMEXP("0i") = 1+0i
Related Videos
See Also
References
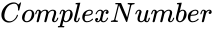 is of the form x+iy.
is of the form x+iy.
 ,
, 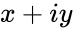 ,
,  &
&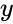 are real numbers &
are real numbers &  is the imaginary unit.
is the imaginary unit. 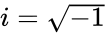 .
. , for any real number
, for any real number 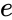 is the base of the natural logarithm.
is the base of the natural logarithm.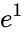 .
.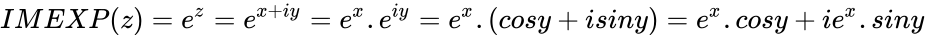 .
.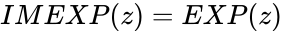 when imaginary number
when imaginary number 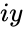 is '0'.
is '0'.