Difference between revisions of "Manuals/calci/IMPOWER"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
(→ZOS) |
||
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''IMPOWER(Complexnumber,n)'''</div><br/> |
| + | *<math>Complexnumber</math> is of the form <math>z=x+iy</math> | ||
| + | *<math>n</math> is the power value. | ||
| + | **IMPOWER(), returns a complex number raised to an integer power. | ||
| − | + | ==Description== | |
| + | *This function gives the value of powers of complex number. | ||
| + | *DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form. | ||
| + | *<math>i</math> is the imaginary unit, <math>i=\sqrt{-1}</math> | ||
| + | *Then the power of a complex number is defined by | ||
| + | :<math>(z)^n=(x+iy)^n=r^n*e^{in\theta}=r^n(cosn\theta+isinn\theta)</math> | ||
| + | where <math>r=\sqrt{x^2+y^2}</math> and <math>\theta=tan^{-1}(\frac{y}{x})</math>, <math>\theta \isin (-\pi,\pi]</math>. | ||
| + | *This formula is called DeMoivre's theorem of complex numbers. | ||
| + | *We can use [[Manuals/calci/COMPLEX| COMPLEX]] function to convert real and imaginary number in to a complex number. | ||
| + | *In IMPOWER(Complexnumber,n), <math>n</math> can be integer, fractional or negative. | ||
| + | *If <math>n</math> is non-numeric, function will return error value. | ||
| − | </ | + | ==ZOS== |
| − | + | *The syntax is to calculate powers of Complex number in ZOS is <math>IMPOWER(Complexnumber,n)</math>. | |
| − | < | + | **<math>Complexnumber</math> is of the form <math>z=x+iy</math> |
| + | **<math>n</math> is the power value. | ||
| + | *For e.g.,IMPOWER("7-8i",6) | ||
| + | {{#ev:youtube|QRkmmsadQhA|280|center|Impower}} | ||
| − | + | ==Examples== | |
| − | + | #=IMPOWER("4+5i",3) = -235.99999+115i | |
| − | --- | + | #=IMPOWER("9-7i",4) = -14852-8063.999999i |
| − | + | #=IMPOWER("6",9) = 10077696+0i | |
| + | #=IMPOWER("i",10) = -1+0i | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|dl_9NC_J6yo|280|center|IMPOWER}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/IMREAL | IMREAL ]] | |
| − | + | *[[Manuals/calci/IMSUM | IMSUM ]] | |
| − | + | *[[Manuals/calci/IMAGINARY | IMAGINARY ]] | |
| + | *[[Manuals/calci/COMPLEX | COMPLEX ]] | ||
| − | + | ==References== | |
| + | [http://en.wikipedia.org/wiki/De_Moivre's_formula De Moivre's formula] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 04:02, 2 November 2020
IMPOWER(Complexnumber,n)
- is of the form
- is the power value.
- IMPOWER(), returns a complex number raised to an integer power.
Description
- This function gives the value of powers of complex number.
- DeMoivre's Theorem is a generalized formula to compute powers of a complex number in it's polar form.
- is the imaginary unit,
- Then the power of a complex number is defined by
where and , .
- This formula is called DeMoivre's theorem of complex numbers.
- We can use COMPLEX function to convert real and imaginary number in to a complex number.
- In IMPOWER(Complexnumber,n), can be integer, fractional or negative.
- If is non-numeric, function will return error value.
ZOS
- The syntax is to calculate powers of Complex number in ZOS is .
- is of the form
- is the power value.
- For e.g.,IMPOWER("7-8i",6)
Examples
- =IMPOWER("4+5i",3) = -235.99999+115i
- =IMPOWER("9-7i",4) = -14852-8063.999999i
- =IMPOWER("6",9) = 10077696+0i
- =IMPOWER("i",10) = -1+0i
Related Videos
See Also
References
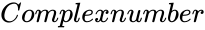 is of the form
is of the form 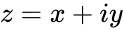
 is the power value.
is the power value.
 is the imaginary unit,
is the imaginary unit, 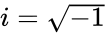
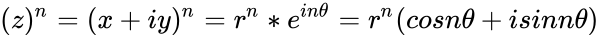
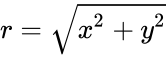 and
and  ,
, ![{\displaystyle \theta \in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/png/2742d923047f035ec3e8db8259485fda0629104b) .
.
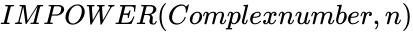 .
.