Difference between revisions of "Manuals/calci/SKEW"
Jump to navigation
Jump to search
(Created page with "<div id="6SpaceContent" class="zcontent" align="left"> <font face="Arial, sans-serif"><font size="2">'''SKEW'''</font></font><font face="Arial, sans-serif"><font size="2">(</...") |
|||
| (20 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''SKEW()'''</div><br/> |
| + | *Parameters are any numbers to calculate the skewness. | ||
| + | **SKEW() returns the skewness of a distribution | ||
| − | + | ==Description== | |
| + | *This function gives the Skewness of a distribution. | ||
| + | *Skewness is a measure of the degree of asymmetry of a distribution. | ||
| + | *A distribution(normal distribution) is symmetry ,it don't have a Skewness. | ||
| + | *In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness. | ||
| + | *If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness. | ||
| + | *In a Left Skewed Distribution, its <math>mean<median<mode</math> | ||
| + | *In a Normal Skewed Distribution, its <math>mean=median=mode</math> | ||
| + | *In a Right Skewed Distribution, its <math>mode<median<mean</math>. | ||
| + | *In <math>SKEW(), First parameter is required.From the second parameter are optional. | ||
| + | *In calci there is no restriction for giving the number of arguments. | ||
| + | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
| + | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | ||
| + | *The equation for Skewness is defined by :<math> Skewness = \frac{n}{(n-1)(n-2)}\sum \left(\frac{x_i-\bar{x}}{s} \right)^3</math> | ||
| + | Where, <math>s</math> is the sample standard deviation, <math>\bar{x}</math> represents a sample mean. | ||
| + | *This function will return the result as error when | ||
| + | 1. Any one of the argument is non-numeric. | ||
| + | 2. If there are fewer than three data points, or the Sample Standard Deviation is zero. | ||
| − | + | ==Examples== | |
| − | + | {| class="wikitable" | |
| − | + | |+Spreadsheet | |
| − | + | |- | |
| − | + | ! !! A !! B !! C !! D!! E | |
| − | + | |- | |
| − | + | ! 1 | |
| − | + | | 0 || 4 || -5 ||4 || 1 | |
| − | + | |- | |
| − | + | ! 2 | |
| − | + | | 29 || 9 || 11 || 5 || 2 | |
| − | + | |- | |
| − | + | ! 3 | |
| − | + | | 41 || 11 || 18 ||2 || 3 | |
| − | + | |- | |
| − | + | ! 4 | |
| − | + | | 18 ||10 || 7 ||5 ||5 | |
| − | + | |- | |
| − | + | ! 5 | |
| − | + | | 4 || 5 || 9 ||6 || 6 | |
| − | + | |- | |
| − | + | ! 6 | |
| − | + | | 38 || 9 || 13 || 8 || 11 | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *=SKEW(B1:B5) = -0.4369344921493 | |
| + | *=SKEW(A1:A6) = -0.21921252920 | ||
| + | *=SKEW(C1:C4) = -0.715957010 | ||
| + | *=SKEW(D1:D6) = 0 | ||
| + | *=SKEW(E1:E6) = 1.16584702768 | ||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|B0xF7UILeKo|280|center|SKEW}} | |
| − | + | ==See Also== | |
| + | *[[Manuals/calci/KURT| KURT]] | ||
| + | *[[Manuals/calci/STDEV | STDEV ]] | ||
| + | *[[Manuals/calci/STDEVP | STDEVP ]] | ||
| − | + | ==References== | |
| + | *[http://en.wikipedia.org/wiki/Skewness Skewness] | ||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[ Z3 | Z3 home ]] | |
| − | |||
Latest revision as of 13:40, 18 June 2018
SKEW()
- Parameters are any numbers to calculate the skewness.
- SKEW() returns the skewness of a distribution
Description
- This function gives the Skewness of a distribution.
- Skewness is a measure of the degree of asymmetry of a distribution.
- A distribution(normal distribution) is symmetry ,it don't have a Skewness.
- In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness.
- If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness.
- In a Left Skewed Distribution, its
- In a Normal Skewed Distribution, its
- In a Right Skewed Distribution, its .
- In
Where, is the sample standard deviation, represents a sample mean.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. If there are fewer than three data points, or the Sample Standard Deviation is zero.
Examples
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 0 | 4 | -5 | 4 | 1 |
| 2 | 29 | 9 | 11 | 5 | 2 |
| 3 | 41 | 11 | 18 | 2 | 3 |
| 4 | 18 | 10 | 7 | 5 | 5 |
| 5 | 4 | 5 | 9 | 6 | 6 |
| 6 | 38 | 9 | 13 | 8 | 11 |
- =SKEW(B1:B5) = -0.4369344921493
- =SKEW(A1:A6) = -0.21921252920
- =SKEW(C1:C4) = -0.715957010
- =SKEW(D1:D6) = 0
- =SKEW(E1:E6) = 1.16584702768
Related Videos
See Also
References
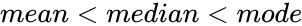
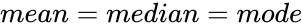
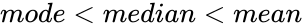 .
.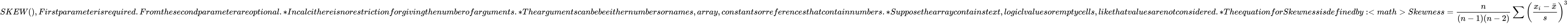
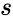 is the sample standard deviation,
is the sample standard deviation, 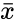 represents a sample mean.
represents a sample mean.