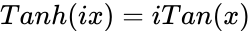Difference between revisions of "Manuals/calci/TANH"
Jump to navigation
Jump to search
(Created page with "<div id="16SpaceContent" align="left"><div class="ZEditBox" align="justify"> Syntax </div></div> ---- <div id="4SpaceContent" align="left"><div class="ZEditBox" align=...") |
|||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <div | + | <div style="font-size:30px">'''TANH(x)'''</div><br/> |
| + | * where x is any real number. | ||
| + | **TANH(), returns the hyperbolic tangent of a number. | ||
| − | + | ==Description== | |
| − | </ | + | *This function gives the hyperbolic Tan of 'x'. |
| − | + | *It is also called as Circular function. | |
| − | < | + | *Here <math>TANH(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}</math> ie, <math>\frac{SINH(x)} {COSH(x)}</math> or <math>-iTAN(ix)</math>, where <math>i</math> is the imginary unit and <math>i=\sqrt{-1}</math> |
| + | *Also relation between Hyperbolic & Trigonometric function is <math>Tan(ix)=iTanh(x)</math> & <math>Tanh(ix)= iTan(x)</math> | ||
| + | *TANH(-x)=-TANH(x) | ||
| − | + | == Examples == | |
| + | '''TANH(x)''' | ||
| + | *'''x''' is any real number. | ||
| − | + | {|id="TABLE1" class="SpreadSheet blue" | |
| − | |||
| − | |||
| − | + | |- class="even" | |
| + | |'''TANH(x)''' | ||
| + | |'''Value''' | ||
| − | + | |- class="odd" | |
| − | - | + | | TANH(0) |
| − | + | | 0 | |
| − | |||
| − | |||
| − | + | |- class="even" | |
| + | | TANH(1) | ||
| + | | 0.7615941559557649 | ||
| − | + | |- class="odd" | |
| − | + | | TANH(10) | |
| − | + | | 1 | |
| − | + | |} | |
| − | |||
| − | + | ==Related Videos== | |
| − | + | {{#ev:youtube|EmJKuQBEdlc|280|center|Hyperbolic TAN}} | |
| − | + | ==See Also== | |
| − | |||
| − | |||
| − | + | *[[Manuals/calci/TAN| TAN]] | |
| − | + | *[[Manuals/calci/SINH| SINH]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Manuals/calci/COSH | COSH]] | |
| − | + | ==References== | |
| − | + | *[http://en.wikipedia.org/wiki/Trigonometric_functions List of Trigonometric Functions] | |
| + | *[http://en.wikipedia.org/wiki/Hyperbolic_function Hyperbolic Function] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | *[[Z_API_Functions | List of Main Z Functions]] | |
| − | + | ||
| − | + | *[[ Z3 | Z3 home ]] | |
Latest revision as of 16:50, 21 August 2018
TANH(x)
- where x is any real number.
- TANH(), returns the hyperbolic tangent of a number.
Description
- This function gives the hyperbolic Tan of 'x'.
- It is also called as Circular function.
- Here ie, or , where is the imginary unit and
- Also relation between Hyperbolic & Trigonometric function is &
- TANH(-x)=-TANH(x)
Examples
TANH(x)
- x is any real number.
| TANH(x) | Value |
| TANH(0) | 0 |
| TANH(1) | 0.7615941559557649 |
| TANH(10) | 1 |
Related Videos
See Also
References
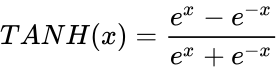 ie,
ie, 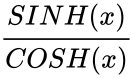 or
or 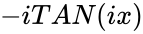 , where
, where  is the imginary unit and
is the imginary unit and 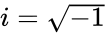
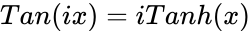 &
&