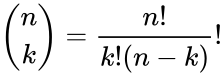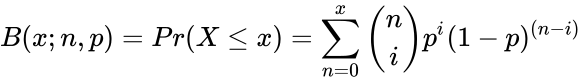Difference between revisions of "Manuals/calci/BINOMDIST"
Jump to navigation
Jump to search
| Line 21: | Line 21: | ||
#<math>ns < 0</math> or <math>ns > ts</math> | #<math>ns < 0</math> or <math>ns > ts</math> | ||
#Also <math>ps < 0</math> or <math>ps >1</math> | #Also <math>ps < 0</math> or <math>ps >1</math> | ||
| + | Example : =BINOMDIST (4, 12, 0.3, FALSE) is 0.2311 | ||
The binomial distribution with parameters n and p, we write <math> X \tilde{} B(n, p)</math>. | The binomial distribution with parameters n and p, we write <math> X \tilde{} B(n, p)</math>. | ||
| Line 27: | Line 28: | ||
The Cumulative Binomial Distribution is:<math>B(x;n,p) = Pr(X \le x) =\sum_{n=0}^x \binom{n}{i}p^{i}(1-p)^{(n-i)}</math> | The Cumulative Binomial Distribution is:<math>B(x;n,p) = Pr(X \le x) =\sum_{n=0}^x \binom{n}{i}p^{i}(1-p)^{(n-i)}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Example== | ==Example== | ||
Revision as of 22:37, 18 November 2013
BINOMDIST (ns, ts, ps, cu)
- is the number of successes in trials.
- is the number of independent trials.
- is the probability of success on each trial
- is a logical value that determines the form of the function.
Description
This function gives the individual element Binomial Distribution Probability.We can use this function when the following conditions are satisfied:
- A number of tests should be fixed.
- Each test must be independent.
- Each test represents only two results(Success/Failure)
- No test has any impact on any other test.
For example, the number of ways to achieve 2 heads in a set of four tosses is "4 choose 2".
- In BINOMDIST function, is the number of successes in trials.
- TS is the number trials to be made, also and should be integers.
- And is number of probability of success on each independent trials.
- Finally is the logical value like TRUE or FALSE. If it is TRUE it will give the cumulative value or FALSE it will give the exact probability.
This function gives result as "Error" when
- and are not an Integer.
- Failed to parse (syntax error): {\displaystyle ns,ts & ps} are not a numeric.
- or
- Also or
Example : =BINOMDIST (4, 12, 0.3, FALSE) is 0.2311
The binomial distribution with parameters n and p, we write . The probability of getting exactly successes in trials is given by the Probability Mass Function: for k=0,1,2,3...n where \binom{n}{k} is the COMBIN(n,k) i.e.
The Cumulative Binomial Distribution is:
Example
- Toss a coin for 12 times. What is the probability of getting exactly 7 heads.
- Here NS=7,TS=12,and PS=1/2=0.5
- BINOMDIST(7,12,0.5,FALSE)=0.193359375
- The LMB Company manufactures tires. They claim that only .007 of LMB tires are defective. What is the probability of finding 2 defective tires in a random sample of 50 LMB tires?
- Here NS=2,TS=50 and PS=0.007
- BINOMDIST(2,50,0.007,false)=0.0428446
| Questions | NS | TS | PS | CU | Result |
|---|---|---|---|---|---|
| Question 1 | 7 | 12 | 0.5(1/2) | False | 0.193359375 |
| Question2 | 2 | 15 | 0.007 | False | 0.0428446 |
 is the number of successes in trials.
is the number of successes in trials. is the number of independent trials.
is the number of independent trials.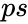 is the probability of success on each trial
is the probability of success on each trial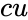 is a logical value that determines the form of the function.
is a logical value that determines the form of the function. should be fixed.
should be fixed.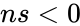 or
or 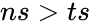
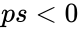 or
or 
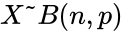 .
The probability of getting exactly
.
The probability of getting exactly  successes in
successes in 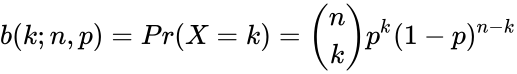 for k=0,1,2,3...n where \binom{n}{k} is the COMBIN(n,k) i.e.
for k=0,1,2,3...n where \binom{n}{k} is the COMBIN(n,k) i.e.