Difference between revisions of "Manuals/calci/IMEXP"
Jump to navigation
Jump to search
| Line 10: | Line 10: | ||
==Examples== | ==Examples== | ||
| − | #IMEXP("2+3i")=-7.315110094901102+1.0427436562359i | + | #=IMEXP("2+3i") = -7.315110094901102+1.0427436562359i |
| − | #IMEXP("4-5i")=15.4874305606508+52.355491418482i | + | #=IMEXP("4-5i") = 15.4874305606508+52.355491418482i |
| − | #IMEXP("6")=403.428793492735 | + | #=IMEXP("6") = 403.428793492735 |
| − | #IMEXP("2i")=-0.416146836547142+0.909297426825682i | + | #=IMEXP("2i") = -0.416146836547142+0.909297426825682i |
| − | #IMEXP("0")=1 | + | #=IMEXP("0") = 1 and IMEXP("0i") = 1 |
==See Also== | ==See Also== | ||
Revision as of 05:14, 25 November 2013
IMEXP(z)
- where is the complex number.
Description
- This function gives the exponential of a complex number.
- In , is the complex number of the form , & are real numbers & is the imaginary unit. .
- Euler's formula states that , for any real number and is the base of the natural logarithm.
- The approximate value of the constant e=2.718281828459045 and it is equal to . So the exponential of a complex number is : .
- When imaginary part is '0', it will give the exponent value of the real number. i.e when imaginary number is '0'.
- We can use COMPLEX function to convert the real and imaginary coefficients to a complex number.
Examples
- =IMEXP("2+3i") = -7.315110094901102+1.0427436562359i
- =IMEXP("4-5i") = 15.4874305606508+52.355491418482i
- =IMEXP("6") = 403.428793492735
- =IMEXP("2i") = -0.416146836547142+0.909297426825682i
- =IMEXP("0") = 1 and IMEXP("0i") = 1
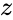 is the complex number.
is the complex number.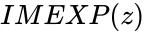 ,
, 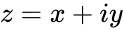 ,
,  &
&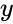 are real numbers &
are real numbers &  is the imaginary unit.
is the imaginary unit. 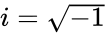 .
. , for any real number
, for any real number 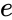 is the base of the natural logarithm.
is the base of the natural logarithm.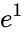 . So the exponential of a complex number is :
. So the exponential of a complex number is : 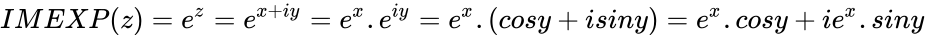 .
.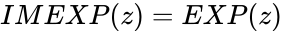 when imaginary number
when imaginary number 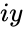 is '0'.
is '0'.