Difference between revisions of "Manuals/calci/FTEST"
Jump to navigation
Jump to search
| Line 15: | Line 15: | ||
==Examples== | ==Examples== | ||
| − | + | 1.DATA1 DATA2 | |
| − | + | 15 21 | |
| − | + | 27 12 | |
| − | + | 19 30 | |
| − | + | 32 11 | |
| − | + | FTEST(B4:B8,C4:C8)=0.81524906747183 | |
| + | 2.DATA 1={5,8,12,45,23}; DATA2={10,20,30,40,50} | ||
| + | FTEST(A1:A5,C1:C5)=0.9583035732212274 | ||
| + | 3. DATA1={14,26,37};DATA2={45,82,21,17} | ||
| + | FTEST(B1:B3,C1:C4}=0.26412211240525474 | ||
| + | 4.DATA1={25},DATA2={45,65} | ||
| + | FTEST(B1,C2:C3)=NAN | ||
==See Also== | ==See Also== | ||
Revision as of 01:01, 10 December 2013
FTEST(ar1,ar2)
- and are array of data.
Description
- This function gives the result of F-test.
- The F-test is designed to test if two population variances are equal.
- It does this by comparing the ratio of two variances.
- So, if the variances are equal, the ratio of the variances will be 1.Let X1, ..., Xn and Y1, ..., Ym be independent samples each have a normal distribution .
- It's sample means: X(bar)=1/n summation(i=1 to n)Xi and Y(bar)=1/m summation(i=1 to m)Yi .
- The sample variances : Sx^2=1/n-1 summation(i=1 to n)(Xi-X(bar))^2.and SY^2=1/m-1 summation(i=1 to m)(Yi-Y(bar))^2.
- Then the test statistic= Sx^2/Sy^2 has an F-distribution with n − 1 and m − 1 degrees of freedom.
- In FTEST(ar1,ar2) where ar1 is the data of first array,ar2 is the data of second array.
- The array may be any numbers, names, or refernces that contains numbers.
- Suppose the array contains any text, logical values or empty cells like that values are not considered.
When the ar or ar2 is less than 2 or the variance of the array value is zero then this function will return the result as error.
Examples
1.DATA1 DATA2
15 21 27 12 19 30 32 11
FTEST(B4:B8,C4:C8)=0.81524906747183 2.DATA 1={5,8,12,45,23}; DATA2={10,20,30,40,50}
FTEST(A1:A5,C1:C5)=0.9583035732212274
3. DATA1={14,26,37};DATA2={45,82,21,17} FTEST(B1:B3,C1:C4}=0.26412211240525474 4.DATA1={25},DATA2={45,65} FTEST(B1,C2:C3)=NAN
See Also
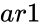 and
and 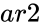 are array of data.
are array of data.