Difference between revisions of "Manuals/calci/LOGNORMDIST"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
*And φ is the cumulative distribution function of the standard normal distribution. | *And φ is the cumulative distribution function of the standard normal distribution. | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. Any one of the argument is nonnumeric. | + | *1. Any one of the argument is nonnumeric. |
| − | 2.suppose <math> x \le 0 </math> or <math> sd \le 0</math | + | *2.suppose <math> x \le 0 </math> or <math> sd \le 0</math> |
| − | |||
| − | |||
| − | + | ==Examples== | |
| + | #LOGNORMDIST(2,5.4,2.76)=0.044061652 | ||
| + | #LOGNORMDIST(10,24.05,12.95)=0.046543186 | ||
| + | #LOGNORMDIST(50,87.0036,42.9784)=0.026597569 | ||
| + | #LOGNORMDIST(-10,5,2)=NAN | ||
| − | + | ==See Also== | |
| − | + | *[[Manuals/calci/LN | LN ]] | |
| − | + | *[[Manuals/calci/LOG10 | LOG10 ]] | |
| + | *[[Manuals/calci/EXP | EXP ]] | ||
| − | |||
| − | + | *[[Manuals/calci/SKEW | SKEW ]] | |
| − | + | *[[Manuals/calci/STDEV | STDEV ]] | |
| − | + | *[[Manuals/calci/STDEVP | STDEVP ]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 00:19, 19 December 2013
LOGNORMDIST((x,m,sd)
- is the value , is the mean of ,
- And is the standard deviation of .
Description
- This function gives the value of the cumulative log normal distribution.
- This distribution is the continuous probability distribution.
- Lognomal distribution is also called Galton's distribution.
- A random variable which is log-normally distributed takes only positive real values.
- Suppose is normally distributed function ,then also normally distributed
- also normally distributed.
- Let the normal distribution function and its mean= Failed to parse (syntax error): {\displaystyle μ} , standard deviation = Failed to parse (syntax error): {\displaystyle σ}
- Then the lognormal cumulative distribution is calculated by:Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,μ,σ)=1/2[1+(erf(ln(x)-μ)/σsqrt(2)= φ[(ln(x)-μ)/σ]} where erf is the error function( the error function (also called the Gauss error function) is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations)
- And φ is the cumulative distribution function of the standard normal distribution.
- This function will give the result as error when
- 1. Any one of the argument is nonnumeric.
- 2.suppose or
Examples
- LOGNORMDIST(2,5.4,2.76)=0.044061652
- LOGNORMDIST(10,24.05,12.95)=0.046543186
- LOGNORMDIST(50,87.0036,42.9784)=0.026597569
- LOGNORMDIST(-10,5,2)=NAN
See Also
 is the value ,
is the value , is the mean of
is the mean of 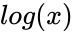 ,
,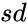 is the standard deviation of
is the standard deviation of 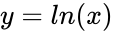 also normally distributed
also normally distributed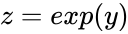 also normally distributed.
also normally distributed.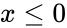 or
or