Difference between revisions of "Manuals/calci/LISTPRIMES"
Jump to navigation
Jump to search
| Line 19: | Line 19: | ||
==Examples== | ==Examples== | ||
| − | #LISTPRIMES(20,11)=11 13 17 19 | + | #LISTPRIMES(20,11) = 11 13 17 19 |
| − | #LISTPRIMES(20,11,3)=17 | + | #LISTPRIMES(20,11,3) = 17 |
| − | #LISTPRIMES(150,130)=131,137,139,149 | + | #LISTPRIMES(150,130) = 131,137,139,149 |
| − | #LISTPRIMES(10,-1)=2 3 5 7 | + | #LISTPRIMES(10,-1) = 2 3 5 7 |
| − | #LISTPRIMES(-10,1)=Null | + | #LISTPRIMES(-10,1) = Null |
| − | #LISTPRIMES(90,70)=71 73 79 83 89 | + | #LISTPRIMES(90,70) = 71 73 79 83 89 |
| − | #LISTPRIMES(90,70,4)=83 | + | #LISTPRIMES(90,70,4) = 83 |
| − | #LISTPRIMES(90,70,6)=Null | + | #LISTPRIMES(90,70,6) = Null |
==See Also== | ==See Also== | ||
Revision as of 00:15, 26 December 2013
LISTPRIMES(max,min,i)
- is the upper limit.
- is the lower limit and i is the position of a prime number.
Description
- This function is listing the set of prime numbers for the given set of numbers.
- A prime number is a natural number, it can be divided, without a remainder, only by itself and by 1.
- For e.g. the number 11 is a prime, because 11 is divided by 1 and 11 without any remainder.
- But 6 is not prime, because 6 can be divided by 1,2,3 and 6. Such numbers are called composite numbers.
- Also the number 0 and 1 are neither prime nor composite.
- In , gives the list of prime numbers between the range and .
- is the upper limit value and is the lower limit value
- And is the position of the prime number value. value is optional.
- Suppose we are not giving the ith value, it will show all the prime numbers in given range.
- This function will give the result as error when
- any one of the argument is nonnumeric.
- or is the beyond the range number of prime numbers
- or .
Examples
- LISTPRIMES(20,11) = 11 13 17 19
- LISTPRIMES(20,11,3) = 17
- LISTPRIMES(150,130) = 131,137,139,149
- LISTPRIMES(10,-1) = 2 3 5 7
- LISTPRIMES(-10,1) = Null
- LISTPRIMES(90,70) = 71 73 79 83 89
- LISTPRIMES(90,70,4) = 83
- LISTPRIMES(90,70,6) = Null
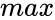 is the upper limit.
is the upper limit.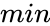 is the lower limit and i is the
is the lower limit and i is the 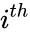 position of a prime number.
position of a prime number.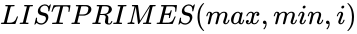 , gives the list of prime numbers between the range
, gives the list of prime numbers between the range  is the position of the prime number value.
is the position of the prime number value. 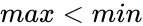 or
or 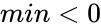 .
.