Difference between revisions of "Manuals/calci/MOD"
Jump to navigation
Jump to search
| Line 4: | Line 4: | ||
==Description== | ==Description== | ||
*This function gives the remainder of the number after dividing with some number. | *This function gives the remainder of the number after dividing with some number. | ||
| − | *When we divide two integers we will get the result like this: X/Y= Q with remainder <math>R</math>. Here <math> X </math> is the dividend, <math>Y</math> is the divisor, <math>Q</math> is the Quotient and <math> R</math> is the remainder.So <math> MOD(n,d)=R</math>. | + | *When we divide two integers we will get the result like this: X/Y= Q with remainder <math>R</math>. Here <math> X </math> is the dividend, <math>Y</math> is the divisor, <math>Q</math> is the Quotient and <math> R</math> is the remainder.So <math> MOD(n,d)=R</math>. |
*For e.g., MOD(5,2)=1. Here 1 is the remainder. | *For e.g., MOD(5,2)=1. Here 1 is the remainder. | ||
*The <math>MOD</math> function we can write using <math>INT</math> function: <math> MOD(n,d)=n-d*INT(n/d)</math>. | *The <math>MOD</math> function we can write using <math>INT</math> function: <math> MOD(n,d)=n-d*INT(n/d)</math>. | ||
Revision as of 21:43, 25 December 2013
MOD(n,d)
- is any real number and is the divisor
Description
- This function gives the remainder of the number after dividing with some number.
- When we divide two integers we will get the result like this: X/Y= Q with remainder . Here is the dividend, is the divisor, is the Quotient and is the remainder.So .
- For e.g., MOD(5,2)=1. Here 1 is the remainder.
- The function we can write using function: .
- This function will return the result as error when the d value is 0.
- Suppose the value of n and d with same sign either '+' or '-',then the result also with same sign.
- But and are with different then the result will come with the sign only.
Examples
- MOD(5,2)=1
- MOD(-11,-3)-2
- MOD(25,5)=0
- MOD(12,-4)=0
- MOD(85,-9)=-5
- MOD(-52,7)=4
- MOD(0,9)=0
- MOD(9,0)=NAN
- MOD(5.5,2)=1.5
 is any real number and
is any real number and 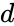 is the divisor
is the divisor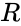 . Here
. Here 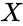 is the dividend,
is the dividend, 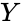 is the divisor,
is the divisor,  is the Quotient and
is the Quotient and 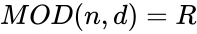 .
.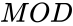 function we can write using
function we can write using 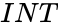 function:
function: 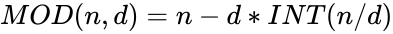 .
.