Difference between revisions of "Manuals/calci/ERF"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*In <math>ERF(ll,ul),ll</math> is the lower limit of the integrating function and <math>ul</math> is the upper limit of the integrating function. | *In <math>ERF(ll,ul),ll</math> is the lower limit of the integrating function and <math>ul</math> is the upper limit of the integrating function. | ||
*Also <math>ul</math> is optional. When we are omitting the <math>ul</math> value, then the integral of the error function between 0 and the given <math>ll</math> value is returned otherwise it will consider the given <math>ll</math> and <math>ul</math> values. | *Also <math>ul</math> is optional. When we are omitting the <math>ul</math> value, then the integral of the error function between 0 and the given <math>ll</math> value is returned otherwise it will consider the given <math>ll</math> and <math>ul</math> values. | ||
| − | *This function is also called Gauss error function.<math>ERF </math>is defined by: <math>ERF(z)=\frac {2}{\sqrt | + | *This function is also called Gauss error function.<math>ERF </math>is defined by: <math>ERF(z)=\frac {2}{\sqrt{&pi}}\int\limits_{0}^{z}e^-t^2 dt</math> |
| − | <math>ERF(a,b)=\frac{2}{\sqrt | + | <math>ERF(a,b)=\frac{2}{\sqrt{&pi}\int\limits_{a}^{b}e^-t^2 dt=ERF(b)-ERF(a)(/math>. |
*In this case 'a' is the lower limit and 'b' is the upper limit. | *In this case 'a' is the lower limit and 'b' is the upper limit. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
Revision as of 22:53, 25 December 2013
ERF(ll,ul)
- is the lower limit and is the upper limit.
Description
- This function gives the value of the error function .
- Error function is the special function which is encountered in integrating the normal distribution.
- In is the lower limit of the integrating function and is the upper limit of the integrating function.
- Also is optional. When we are omitting the value, then the integral of the error function between 0 and the given value is returned otherwise it will consider the given and values.
- This function is also called Gauss error function.is defined by: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ERF(z)=\frac {2}{\sqrt{&pi}}\int\limits_{0}^{z}e^-t^2 dt}
<math>ERF(a,b)=\frac{2}{\sqrt{&pi}\int\limits_{a}^{b}e^-t^2 dt=ERF(b)-ERF(a)(/math>.
- In this case 'a' is the lower limit and 'b' is the upper limit.
- This function will return the result as error when
- any one of the argument is nonnumeric.
- ll or ul is negative.
Examples
- ERF(1,2)=0.15262153
- ERF(3,2)=-0.004655645
- ERF(0,1)=0.842700735
- ERF(5)=1
- ERF(-3)=NAN
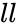 is the lower limit and
is the lower limit and 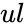 is the upper limit.
is the upper limit.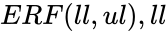 is the lower limit of the integrating function and
is the lower limit of the integrating function and 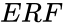 is defined by: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ERF(z)=\frac {2}{\sqrt{&pi}}\int\limits_{0}^{z}e^-t^2 dt}
is defined by: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ERF(z)=\frac {2}{\sqrt{&pi}}\int\limits_{0}^{z}e^-t^2 dt}