Difference between revisions of "Manuals/calci/SKEW"
Jump to navigation
Jump to search
| Line 16: | Line 16: | ||
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
*Suppose the array contains text,logicl values or empty cells, like that values are not considered. | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | ||
| − | *The equation for skewness is defined by :<math> Skewness= \frac{3(mean-median)}{s}</math> OR <math>skewness= \ | + | *The equation for skewness is defined by :<math> Skewness= \frac{3(mean-median)}{s}</math> OR <math>skewness= \tfrac{\sum (x_i-\bar{x})^3}{(N-1)s^3}</math> Where: s is the sample standard deviation, <math>\bar{x}</math> represents a sample mean. |
*This function will return the result as error when | *This function will return the result as error when | ||
1. Any one of the argument is nonnumeric. | 1. Any one of the argument is nonnumeric. | ||
Revision as of 03:36, 17 January 2014
SKEW(n1,n2,…)
- Failed to parse (syntax error): {\displaystyle n1,n2,…} are numbers to calculate the skewness.
Description
- This function gives the skewness of a distribution.
- Skewness is a measure of the degree of asymmetry of a distribution.
- A distribution(normal ditribution) is symmetry ,it don't have a skewness.
- In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have negative skewness.
- In a distribution is skewed to the right , the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness.
- In a left skewed distribution ,its mean<median<mode.
- In a normal skewed distribution, its mean=median=mode.
- In a right skewed distribution, its mode<median<mean.
- In is required. are optional.
- In calci there is no restriction for giving the number of arguments.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logicl values or empty cells, like that values are not considered.
- The equation for skewness is defined by : OR Where: s is the sample standard deviation, represents a sample mean.
- This function will return the result as error when
1. Any one of the argument is nonnumeric. 2. If there are fewer than three data points, or the sample standard deviation is zero.
where
SKEW(n1,n2,...)
Where n1, n2 ... are numbers to calculate the skewness.
It calculates the skewness of a distribution.
- If the data points are less than three,the function displays NaN.
- The equation for skewness is:
SKEW
C1R1=13
C2R2=14
C3R3=15
C4R4=12
C5R5=13
C6R6=14
C7R7=9
C8R8=16
C9R9=14
C10R10=17
i.e.SKEW(Column1Row1:Column1Row10)
i.e.= SKEW(C1R1:C1R10) is -0.756
Syntax
Remarks
Examples
Description
| Column1 | Column2 | Column3 | Column4 | |
| Row1 | 13 | -0.756 | ||
| Row2 | 14 | |||
| Row3 | 15 | |||
| Row4 | 12 | |||
| Row5 | 13 | |||
| Row6 | 14 | |||
| Row7 | 9 | |||
| Row8 | 16 | |||
| Row9 | 14 | |||
| Row10 | 17 |
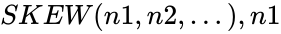 is required.
is required.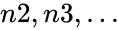 are optional.
are optional.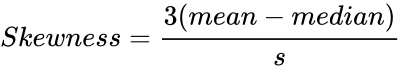 OR
OR 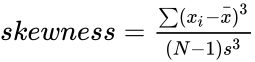 Where: s is the sample standard deviation,
Where: s is the sample standard deviation, 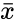 represents a sample mean.
represents a sample mean.