Difference between revisions of "Manuals/calci/REGRESSION"
Jump to navigation
Jump to search
| Line 32: | Line 32: | ||
==Examples== | ==Examples== | ||
#Temperature - Drying time(hours) | #Temperature - Drying time(hours) | ||
| − | 54 | + | 54 - 8 |
| − | 63 | + | 63 - 6 |
| − | 75 | + | 75 - 3 |
| − | 82 | + | 82 - 1 |
=REGRESSIONANALYSIS(A1:A4,B1:B4)= | =REGRESSIONANALYSIS(A1:A4,B1:B4)= | ||
| − | Unit sales | + | Unit sales - Ads - population |
| − | 4000 | + | 4000 - 12000 - 300000 |
| − | 5200 | + | 5200 - 13150 - 411000 |
| − | 6800 | + | 6800 - 14090 - 500000 |
| − | 8000 | + | 8000 - 11900 - 650000 |
| − | 10000 | + | 10000 - 15000 - 800000 |
| + | =REGRESSIONANALYSIS(B1:B5,C1:D5)= | ||
| − | + | ==See Also== | |
| − | |||
| − | |||
| − | + | ==References== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Revision as of 09:47, 20 January 2014
REGRESSIONANALYSIS(y,x)
- is the set of dependent variables .
- is the set of independent variables.
Description
- This function is calculating the Regression analysis of the given data.
- This analysis is very useful for the analyzation of large amounts of data and making predictions.
- This analysis give the result in three table values.
- Regression statistics table.
- ANOVA table.
- Residual output.
- 1.Regression statistics :
- It contains multiple R, R Square, Adjusted R Square, Standard Error and observations.
- R square gives the fittness of the data with the regression line.
- That value is closer to 1 is the better the regression line fits the data.
- Standard Error refers to the estimated standard deviation of the error term. It is called the standard error of the regression.
- 2.ANOVA table:
- ANOVA is the analysis of variance.
- This table splits in to two components which is Residual and Regression.
- Total sum of squares= Residual (error) sum of squares+ Regression (explained) sum of squares.
- Also this table gives the probability, T stat, significance of F and P.
- When the significance of F is < 0.05, then the result for the given data is statistically significant.
- When the significance of F is > 0.05, then better to stop using this set of independent variables.
- Then remove a variable with a high P-value and returnun the regression until Significance F drops below 0.05.
- So the Significance of P value should be <0.05.
- This table containing the regression coefficient values also.
- 3.Residual output:
- The residuals show you how far away the actual data points are fom the predicted data points.
Examples
- Temperature - Drying time(hours)
54 - 8 63 - 6 75 - 3 82 - 1
REGRESSIONANALYSIS(A1:A4,B1:B4)
Unit sales - Ads - population 4000 - 12000 - 300000 5200 - 13150 - 411000 6800 - 14090 - 500000 8000 - 11900 - 650000 10000 - 15000 - 800000
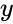 is the set of dependent variables .
is the set of dependent variables . is the set of independent variables.
is the set of independent variables.