Difference between revisions of "Manuals/calci/SKEW"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''SKEW(n1,n2,…)'''</div><br/> | <div style="font-size:30px">'''SKEW(n1,n2,…)'''</div><br/> | ||
*<math>n_1,n_2,…</math> are numbers to calculate the skewness. | *<math>n_1,n_2,…</math> are numbers to calculate the skewness. | ||
| − | |||
==Description== | ==Description== | ||
| − | *This function gives the | + | *This function gives the Skewness of a distribution. |
*Skewness is a measure of the degree of asymmetry of a distribution. | *Skewness is a measure of the degree of asymmetry of a distribution. | ||
| − | *A distribution(normal | + | *A distribution(normal distribution) is symmetry ,it don't have a Skewness. |
| − | *In a distribution the left tail is more pronounced than the right tail | + | *In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness. |
| − | * | + | *If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness. |
| − | *In a left skewed distribution ,its mean<median<mode | + | *In a left skewed distribution ,its <math>mean<median<mode</math> |
| − | *In a normal skewed distribution, its mean=median=mode | + | *In a normal skewed distribution, its <math>mean=median=mode</math> |
| − | *In a right skewed distribution, its mode<median<mean. | + | *In a right skewed distribution, its <math>mode<median<mean</math>. |
| − | *In <math>SKEW(n_1,n_2,...), n_1</math> | + | *In <math>SKEW(n_1,n_2,...), n_1</math> is required.<math>n_2,n_3,...</math> are optional. |
*In calci there is no restriction for giving the number of arguments. | *In calci there is no restriction for giving the number of arguments. | ||
*The arguments can be be either numbers or names, array,constants or references that contain numbers. | *The arguments can be be either numbers or names, array,constants or references that contain numbers. | ||
*Suppose the array contains text,logicl values or empty cells, like that values are not considered. | *Suppose the array contains text,logicl values or empty cells, like that values are not considered. | ||
| − | *The equation for | + | *The equation for Skewness is defined by :<math> Skewness = \frac{n}{(n-1)(n-2)}\sum \left(\frac{x_i-\bar{x}}{s} \right)^3</math> |
| + | Where, <math>s</math> is the sample standard deviation, <math>\bar{x}</math> represents a sample mean. | ||
*This function will return the result as error when | *This function will return the result as error when | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non-numeric. |
| − | 2. If there are fewer than three data points, or the | + | 2. If there are fewer than three data points, or the Sample Standard Deviation is zero. |
==Examples== | ==Examples== | ||
| Line 32: | Line 32: | ||
5.Array={1,2,3,5,6,11} | 5.Array={1,2,3,5,6,11} | ||
SKEW(A1:A6)=1.16584702768 | SKEW(A1:A6)=1.16584702768 | ||
| − | |||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 01:52, 21 January 2014
SKEW(n1,n2,…)
- Failed to parse (syntax error): {\displaystyle n_1,n_2,…} are numbers to calculate the skewness.
Description
- This function gives the Skewness of a distribution.
- Skewness is a measure of the degree of asymmetry of a distribution.
- A distribution(normal distribution) is symmetry ,it don't have a Skewness.
- In a distribution the left tail is more pronounced than the right tail (towards more negative values) then the function is said to have Negative Skewness.
- If a distribution is skewed to the right, the tail on the curve's right-hand side is longer than the tail on the left-hand side (towards more positive values), then the function is said to have a positive skewness.
- In a left skewed distribution ,its
- In a normal skewed distribution, its
- In a right skewed distribution, its .
- In is required. are optional.
- In calci there is no restriction for giving the number of arguments.
- The arguments can be be either numbers or names, array,constants or references that contain numbers.
- Suppose the array contains text,logicl values or empty cells, like that values are not considered.
- The equation for Skewness is defined by :
Where, is the sample standard deviation, represents a sample mean.
- This function will return the result as error when
1. Any one of the argument is non-numeric. 2. If there are fewer than three data points, or the Sample Standard Deviation is zero.
Examples
1.Array={4,9,11,10,5} SKEW(B1:B5)=-0.4369344921493 2.Array={0,29,41,18,4,38} SKEW(A1:A6)=-0.21921252920 3.Array={-5,11,18,7} SKEW(C1:C4)=-0.715957010 4.Array={4,5,2,5,6,8} SKEW(C1:C6)=0 5.Array={1,2,3,5,6,11} SKEW(A1:A6)=1.16584702768
See Also
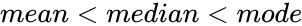
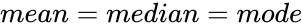
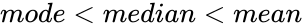 .
.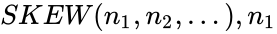 is required.
is required.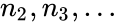 are optional.
are optional.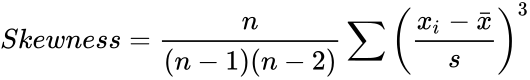
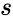 is the sample standard deviation,
is the sample standard deviation, 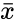 represents a sample mean.
represents a sample mean.