Difference between revisions of "Manuals/calci/SQRTPI"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*<math> PI()</math> is denoted by the Greek letter <math> \pi</math>. | *<math> PI()</math> is denoted by the Greek letter <math> \pi</math>. | ||
*<math> \pi </math> is a transcendental number and irrational number. | *<math> \pi </math> is a transcendental number and irrational number. | ||
| − | *Being an irrational number,<math> | + | *Being an irrational number, <math> \pi </math> cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the <math> \pi </math> value, also no fraction can be its exact value. |
| − | This function will give the result as error when n<0. | + | This function will give the result as error when <math>n<0</math>. |
==Examples== | ==Examples== | ||
Revision as of 00:26, 5 February 2014
SQRTPI(n)
- is the number.
Description
- This function gives the square root of .
- The is a mathematical constant with a value approximate to 3.14159.
- In , is the number by which is multiplied. When we are omitting the value of , then it will consider the value .
- is denoted by the Greek letter .
- is a transcendental number and irrational number.
- Being an irrational number, cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the value, also no fraction can be its exact value.
This function will give the result as error when .
Examples
- =SQRTPI(1) = 1.772453851
- =SQRTPI(0) = 0
- =SQRTPI(5) = 3.963327298
- =SQRTPI(-2) = NAN
See Also
 is the number.
is the number.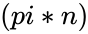 .
.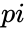 is a mathematical constant with a value approximate to 3.14159.
is a mathematical constant with a value approximate to 3.14159.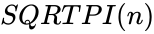 ,
, 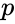 is multiplied. When we are omitting the value of
is multiplied. When we are omitting the value of 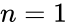 .
.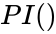 is denoted by the Greek letter
is denoted by the Greek letter 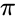 .
.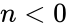 .
.