Difference between revisions of "Manuals/calci/tan"
| Line 197: | Line 197: | ||
0 &for &x>b | 0 &for &x>b | ||
\end{cases}</math> | \end{cases}</math> | ||
| + | ==Video== | ||
| + | {{Infopage|WP:VIDEO}} | ||
| + | :''This is modeled on [[Wikipedia:Images]], and is still very much a work in progress.'' | ||
| − | | + | [[File:Videoonwikipedia.ogv|thumb|thumbtime=0:58|right|320px|Tutorial video for 'Video on Wikipedia' (''how very meta!'')]] |
| + | [[File:Gct.ogg|thumb |320px | alt=Example alt text |[[Grand Central Terminal]] (example video)<br>Example caption for video<br/><hr/>''To produce this box, use:''<br />UNIQ9261d52fb74861f1-code-00000003-QINU]] | ||
| + | [[File:Physicsworks.ogg|thumb|320px|alt="physics works! video"|Video from an MIT course lecture by [[w:Walter Lewin|Walter Lewin]] on the conservation of mechanical energy.]] | ||
| + | [[Wikipedia:About|Wikipedia]] is still at an early stage in its process of incorporating '''[[video]]s''' into its encyclopedic content. This page gives a very brief overview of how videos are used in Wikipedia; for more information, see ''[[Wikipedia:Image use policy|Images guideline]]'' and ''[[Wikipedia:Image use policy|Image use policy]]'', and see ''[[Help:Files]]'' on how to upload and include an video. | ||
| + | |||
| + | '''Most video activity is currently through [[Wikipedia:WikiProject Wiki Makes Video]]'''. | ||
| + | |||
| + | The impetus for starting this page was the [[Wikipedia:Lights Camera Wiki]] video initiative, which should lead to a good expansion of video content. | ||
==Trial 4== | ==Trial 4== | ||
Revision as of 02:46, 3 March 2014
- where n is in Radians
- by default Calci use Radian as angle
DTAN can be used if the angle is in degrees.
The angle can be a single value or any complex array of values. TAN= SIN / COS
For example TAN(1..100) can give an array of the results, which is the TAN value for each of the elements in the array. The array could be of any shape.
Failed to parse (syntax error): {\displaystyle f(x,r1,r2)=\Gamma[(r1+r2)/2](r1/r2)^r1/2*(x)r1/2-1/ Γ(r1/2)Γ(r2/2)(1+r1x/r2)^(r1+r2)/2, ==Description== <math>F(x,\lambda)=\begin{cases} 1-e^{-\lambda x} &, x \ge 0 \\ 0 &, x<0 \end{cases}}
Failed to parse (syntax error): {\displaystyle {\frac{n(n+1)}{(n-1)(n-2)(n-3)}*\frac{\sum{\frac{(xi-\bar{x})^4}{s}}\frac{-3(n-1)^2}{(n-2)(n-3)}}
Examples
- Example 1
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 7 | 9 | 15 |
| 2 | 8 | 12 | 13 | 20 | 25 |
| 3 | 14 | 3 | 9 | 6 | 15 |
| 4 | 12 | 23 | 1 | 42 | 17 |
| 5 | 11 | 20 | 9 | 78 | 25 |
From the above table values:
| 15 | 21 | 24 |
| 24 | -30 | 54 |
- Example 2
| 7 | 5 |
| 2 | 3 |
| 6 | 0 |
| 9 | 8 |
| 8 | -4 | 11 |
| 2 | 7 | 5 |
- Here Matrix A is of order 4x2 and Matrix B is of order 2x3.
- So the Product Matrix is of order 4x3. i.e
1st Row 7*8+5*2 = 66 ; 7*(-4)+5*7 = 7 ; 7*11+5*5 = 102 2nd Row 2*8+3*2 = 22 ; 2*(-4)+3*7 = 13 ; 2*11+3*5 = 37 and so on
- =MMULT(B2:C5,D2:F3) gives
| 66 | 7 | 102 |
| 22 | 13 | 37 |
| 48 | -24 | 66 |
| 88 | 20 | 139 |
trial
Failed to parse (syntax error): {\displaystyle F(x,\mu,σ)=\frac{1}{2} \left[1+ erf \left (\frac{ln(x)-μ)}{σ\sqrt{2}}\right)\right ]= φ\left[\frac{ln(x)-μ}{σ}\right ]}
\begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}
Then |A|=a|e f -b|d f +c|d e
h i| g i| g h|
Trial 2
Failed to parse (syntax error): {\displaystyle f(x,r1,r2)=Γ[(r1+r2)/2](r1/r2)^{r1/2}*(x)^{r1/2-1}/ Γ(r1/2)Γ(r2/2)(1+r1x/r2)^(r1+r2)/2}
trial
1..10@DSIN
| v11031 | DSIN |
|---|---|
| 1 | 0.01745240643728351 |
| 2 | 0.03489949670250097 |
| 3 | 0.05233595624294383 |
| 4 | 0.0697564737441253 |
| 5 | 0.08715574274765817 |
| 6 | 0.10452846326765346 |
| 7 | 0.12186934340514748 |
| 8 | 0.13917310096006544 |
| 9 | 0.15643446504023087 |
| 10 | 0.17364817766693033 |
TRIAL3
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Double subscripts: use braces to clarify"): {\displaystyle s_{x}_{1}}
Description
- This function gives the probability of the uniform distribution.
- Uniform distribution is a symmetric probability distribution.
- It is also called rectangular distribution.
- In , is the numeric value to find the probability of the distribution, is the lower limit value and is the upper limit value.
- The probability density function of the uniform distribution in the interval [a,b] are :
Video
- This is modeled on Wikipedia:Images, and is still very much a work in progress.
Example caption for video
To produce this box, use:
?UNIQ9261d52fb74861f1-code-00000003-QINU?
Wikipedia is still at an early stage in its process of incorporating videos into its encyclopedic content. This page gives a very brief overview of how videos are used in Wikipedia; for more information, see Images guideline and Image use policy, and see Help:Files on how to upload and include an video.
Most video activity is currently through Wikipedia:WikiProject Wiki Makes Video.
The impetus for starting this page was the Wikipedia:Lights Camera Wiki video initiative, which should lead to a good expansion of video content.
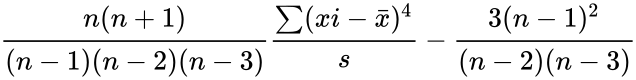
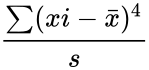
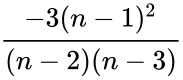
![{\displaystyle F(x,\mu ,\sigma )={\frac {1}{2}}\left[1+erf\left({\frac {ln(x)-\mu )}{\sigma {\sqrt {2}}}}\right)\right]=\varphi \left[{\frac {ln(x)-\mu }{\sigma }}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/png/52b64b4678d5c128bfb328f7005a734bed36e0b6)
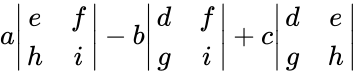
^{\frac {r1}{2}}}{\Gamma ({\frac {r1}{2}})\Gamma ({\frac {r2}{2}})}}*{\frac {(x)^{{\frac {r1}{2}}-1}}{({\frac {1+r1x}{r2}})^{\frac {r1+r2}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/0153606de31a6940e0ec0fc74057de123e7e0e2c)
^{\tfrac {r_{1}}{2}}}{\Gamma ({\frac {r_{1}}{2}})\Gamma ({\frac {r_{2}}{2}})}}*{\frac {(x)^{{\tfrac {r_{1}}{2}}-1}}{({\frac {1+r_{1}x}{r_{2}}})^{\tfrac {r_{1}+r_{2}}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/png/bf128c19052b2d77e9867508e60f25c553dfee41)
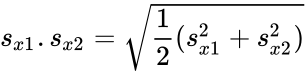
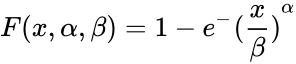
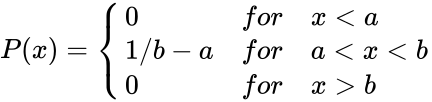
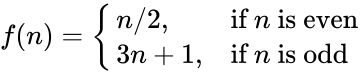
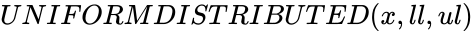 ,
, is the numeric value to find the probability of the distribution,
is the numeric value to find the probability of the distribution, 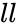 is the lower limit value and
is the lower limit value and 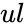 is the upper limit value.
is the upper limit value.