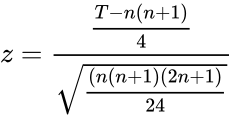Difference between revisions of "Manuals/calci/WILCOXONSIGNEDRANKTEST"
Jump to navigation
Jump to search
(Created page with "==Feature==") |
|||
| Line 1: | Line 1: | ||
| − | == | + | <div style="font-size:30px">'''WILCOXONSIGNEDRANKTEST(xRange,yRange,Confidencelevel,Logicalvalue)'''</div><br/> |
| + | *<math>xRange</math> is the array of x values. | ||
| + | *<math>yRange</math> is the array of y values. | ||
| + | *<math>Confidencelevel</math> is the value between 0 and 1. | ||
| + | *<math>Logicalvalue</math> is either TRUE or FALSE. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the summary values of Wilcoxon signed rank test. | ||
| + | *This test is the one of the Non Parametric test. | ||
| + | *Nonparametric test is also called Distribution Free Test. | ||
| + | *So Wilcoxon Rank test is not depending on the parameters. | ||
| + | *This test is designed to test a hypothesis about the median of a population distribution. | ||
| + | *It often involves the use of matched pairs, for example, before and after data, in which case it tests for a median difference of zero. | ||
| + | *Also this test does not require the assumption that the population is normally distributed. | ||
| + | *This test is the alternative of the Student's T-test. | ||
| + | *Normally this test is the version of the dependent samples t-test that can be performed on the ranked data. | ||
| + | *i.e., When the requirements for the t-test for two paired samples are not satisfied, the Wilcoxon Signed-Rank Test for Paired Samples non-parametric test can often be used. | ||
| + | *It is a more powerful alternative to the sign test, but does assume that the population probability distribution is symmetric. | ||
| + | *For this test let us consider the n subjects from the population with two observations <math>{x_1,x_2,....x_n}</math> and <math>{y_1,y_2,....y_n}</math>. | ||
| + | *The requirements for the Wilcoxon Signed-Rank Tests for Paired Samples where <math>z_i = y_i–x_i</math> for all i = 1, … ,n, are as follows: | ||
| + | 1.the z_i are independent. | ||
| + | 2.x_i and y_i are interval data. | ||
| + | *This test containing the following steps: | ||
| + | *1.Define Null and Alternative hypothesis: | ||
| + | **Null hypothesis <math>H_0</math> = There is no difference between the two observations. | ||
| + | **Alternative hypothesis <math>H_1</math> = There is a difference between the two observations. | ||
| + | *2.State alpha(Confidence level): alpha value is from 0 to 1. | ||
| + | *3.State Decision Rule: Fix the hypothesis value according to the z table. | ||
| + | *4.Calculate Test Statistic:<math>z=\frac{\frac{T-n(n+1)}{4}}{\sqrt{\frac{(n(n+1)(2n+1)}{24}}}</math> | ||
| + | where T is the smallest rank value and n is the number of observations. | ||
| + | *5.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value. | ||
| + | *6.State Conclusion: How far the value of the test before and after the grouping. | ||
| + | *The Wilcoxon signed Rank test result is contains the following values in the table:Difference of the ach observation, Absolute value of the difference,Rank value,Signed Rank and the test value. | ||
| + | |||
| + | ==Examples== | ||
Revision as of 05:05, 6 May 2014
WILCOXONSIGNEDRANKTEST(xRange,yRange,Confidencelevel,Logicalvalue)
- is the array of x values.
- is the array of y values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the summary values of Wilcoxon signed rank test.
- This test is the one of the Non Parametric test.
- Nonparametric test is also called Distribution Free Test.
- So Wilcoxon Rank test is not depending on the parameters.
- This test is designed to test a hypothesis about the median of a population distribution.
- It often involves the use of matched pairs, for example, before and after data, in which case it tests for a median difference of zero.
- Also this test does not require the assumption that the population is normally distributed.
- This test is the alternative of the Student's T-test.
- Normally this test is the version of the dependent samples t-test that can be performed on the ranked data.
- i.e., When the requirements for the t-test for two paired samples are not satisfied, the Wilcoxon Signed-Rank Test for Paired Samples non-parametric test can often be used.
- It is a more powerful alternative to the sign test, but does assume that the population probability distribution is symmetric.
- For this test let us consider the n subjects from the population with two observations and .
- The requirements for the Wilcoxon Signed-Rank Tests for Paired Samples where Failed to parse (syntax error): {\displaystyle z_i = y_i–x_i} for all i = 1, … ,n, are as follows:
1.the z_i are independent.
2.x_i and y_i are interval data.
- This test containing the following steps:
- 1.Define Null and Alternative hypothesis:
- Null hypothesis = There is no difference between the two observations.
- Alternative hypothesis = There is a difference between the two observations.
- 2.State alpha(Confidence level): alpha value is from 0 to 1.
- 3.State Decision Rule: Fix the hypothesis value according to the z table.
- 4.Calculate Test Statistic:
where T is the smallest rank value and n is the number of observations.
- 5.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value.
- 6.State Conclusion: How far the value of the test before and after the grouping.
- The Wilcoxon signed Rank test result is contains the following values in the table:Difference of the ach observation, Absolute value of the difference,Rank value,Signed Rank and the test value.
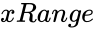 is the array of x values.
is the array of x values.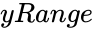 is the array of y values.
is the array of y values.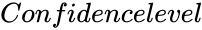 is the value between 0 and 1.
is the value between 0 and 1.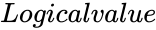 is either TRUE or FALSE.
is either TRUE or FALSE.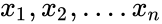 and
and 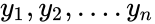 .
.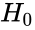 = There is no difference between the two observations.
= There is no difference between the two observations.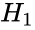 = There is a difference between the two observations.
= There is a difference between the two observations.