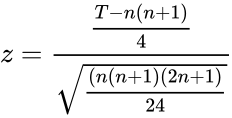Difference between revisions of "Manuals/calci/WILCOXONSIGNEDRANKTEST"
Jump to navigation
Jump to search
| Line 34: | Line 34: | ||
==Examples== | ==Examples== | ||
| + | {| class="wikitable" | ||
| + | |+Spreadsheet | ||
| + | |- | ||
| + | ! !! A !! B !! | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 15 || 18 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 20 || 26 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 29 || 32 | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 30 || 28 | ||
| + | |- | ||
| + | !5 | ||
| + | | 19 || 16 | ||
| + | |} | ||
| + | =WILCOXONSIGNEDRANKTEST(A1:A5,B1:B5,0.05,TRUE) | ||
Revision as of 05:14, 6 May 2014
WILCOXONSIGNEDRANKTEST(xRange,yRange,Confidencelevel,Logicalvalue)
- is the array of x values.
- is the array of y values.
- is the value between 0 and 1.
- is either TRUE or FALSE.
Description
- This function gives the summary values of Wilcoxon signed rank test.
- This test is the one of the Non Parametric test.
- Nonparametric test is also called Distribution Free Test.
- So Wilcoxon Rank test is not depending on the parameters.
- This test is designed to test a hypothesis about the median of a population distribution.
- It often involves the use of matched pairs, for example, before and after data, in which case it tests for a median difference of zero.
- Also this test does not require the assumption that the population is normally distributed.
- This test is the alternative of the Student's T-test.
- Normally this test is the version of the dependent samples t-test that can be performed on the ranked data.
- i.e., When the requirements for the t-test for two paired samples are not satisfied, the Wilcoxon Signed-Rank Test for Paired Samples non-parametric test can often be used.
- It is a more powerful alternative to the sign test, but does assume that the population probability distribution is symmetric.
- For this test let us consider the n subjects from the population with two observations and .
- The requirements for the Wilcoxon Signed-Rank Tests for Paired Samples where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_i = y_i–x_i} for all i = 1, … ,n, are as follows:
1.the are independent. 2. and are interval data.
- This test containing the following steps:
- 1.Define Null and Alternative hypothesis:
- Null hypothesis = There is no difference between the two observations.
- Alternative hypothesis = There is a difference between the two observations.
- 2.State alpha(Confidence level): alpha value is from 0 to 1.
- 3.State Decision Rule: Fix the hypothesis value according to the z table.
- 4.Calculate Test Statistic:
where T is the smallest rank value and n is the number of observations.
- 5.State Result: In this step we have to take a decision of null hypothesis either accept or reject depending on the z value.
- 6.State Conclusion: How far the value of the test before and after the grouping.
- The Wilcoxon signed Rank test result is contains the following values in the table:Difference of the ach observation, Absolute value of the difference,Rank value,Signed Rank and the test value.
Examples
| A | B | ||
|---|---|---|---|
| 1 | 15 | 18 | |
| 2 | 20 | 26 | |
| 3 | 29 | 32 | |
| 4 | 30 | 28 | |
| 5 | 19 | 16 |
=WILCOXONSIGNEDRANKTEST(A1:A5,B1:B5,0.05,TRUE)
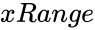 is the array of x values.
is the array of x values.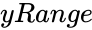 is the array of y values.
is the array of y values.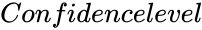 is the value between 0 and 1.
is the value between 0 and 1.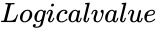 is either TRUE or FALSE.
is either TRUE or FALSE.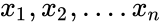 and
and 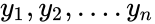 .
.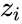 are independent.
2.
are independent.
2.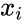 and
and 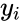 are interval data.
are interval data.
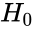 = There is no difference between the two observations.
= There is no difference between the two observations.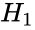 = There is a difference between the two observations.
= There is a difference between the two observations.