Difference between revisions of "Manuals/calci/RIEMANNZETA"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''RIEMANNZETA'''</div><br/>") |
|||
| Line 1: | Line 1: | ||
| − | <div style="font-size:30px">'''RIEMANNZETA'''</div><br/> | + | <div style="font-size:30px">'''RIEMANNZETA(s)'''</div><br/> |
| + | *<math>s</math> is the value from 0 10 infinity. | ||
| + | |||
| + | ==Description== | ||
| + | *This function gives the result for the function of Riemann-Zeta function. | ||
| + | *It is also known as Euler-Riemann Zeta function. | ||
| + | *This function is useful in number theory for the investigating properties of prime numbers. | ||
| + | *It is denoted by <math>\zeta(s)</math>. | ||
| + | *This function is defined as the infinite series ζ(s)=1+2^-s+3^-s+..... | ||
| + | *When the value of s=1,then this series is called the harmonic series. | ||
| + | *When it is increase without any bound or limit, then its sum is infinite. | ||
| + | *When the value of s is larger than 1,the the series converges to a finite number as successive terms are added. | ||
| + | *The riemann zeta function is defined for Complex numbers also. | ||
| + | *So ζ(s) is a function of a complex variable s = σ + it. | ||
| + | *It is a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1. | ||
| + | *It is defined by :ζ(s)=summation n= 1 to infinity n^-s= 1/1^s+1/2^s+1/3^s+..... where σ =Real part of s>1. | ||
| + | *We can define this by integral also:ζ(s)=1/gamma (s)integral 0 to infinity x^(s-1)/e^x-1 dx. | ||
| + | *Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1. | ||
| + | *(For special values:(i)Any positive integer 2n.for n ≥ 1)so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1. | ||
| + | *For odd positive integers, no such simple expression is known. | ||
| + | **When s=1,then ζ (1) is Harmonic series. | ||
| + | **when s=2, then ζ (2) derivation is Basel problem. | ||
| + | **when s=3, then ζ (3) derivation is Apery's constant. | ||
| + | **When s=4, then ζ (4) derivation is Planck's law | ||
Revision as of 23:44, 24 July 2014
RIEMANNZETA(s)
- is the value from 0 10 infinity.
Description
- This function gives the result for the function of Riemann-Zeta function.
- It is also known as Euler-Riemann Zeta function.
- This function is useful in number theory for the investigating properties of prime numbers.
- It is denoted by .
- This function is defined as the infinite series ζ(s)=1+2^-s+3^-s+.....
- When the value of s=1,then this series is called the harmonic series.
- When it is increase without any bound or limit, then its sum is infinite.
- When the value of s is larger than 1,the the series converges to a finite number as successive terms are added.
- The riemann zeta function is defined for Complex numbers also.
- So ζ(s) is a function of a complex variable s = σ + it.
- It is a function of a complex variable s that analytically continues the sum of the infinite series , which converges when the real part of s is greater than 1.
- It is defined by :ζ(s)=summation n= 1 to infinity n^-s= 1/1^s+1/2^s+1/3^s+..... where σ =Real part of s>1.
- We can define this by integral also:ζ(s)=1/gamma (s)integral 0 to infinity x^(s-1)/e^x-1 dx.
- Riemann zeta function is a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1.
- (For special values:(i)Any positive integer 2n.for n ≥ 1)so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1.
- For odd positive integers, no such simple expression is known.
- When s=1,then ζ (1) is Harmonic series.
- when s=2, then ζ (2) derivation is Basel problem.
- when s=3, then ζ (3) derivation is Apery's constant.
- When s=4, then ζ (4) derivation is Planck's law
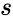 is the value from 0 10 infinity.
is the value from 0 10 infinity.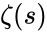 .
.