Difference between revisions of "Manuals/calci/PERMUTATION"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*This matrix has exactly one entry 1 in each row and each column and 0's elsewhere. | *This matrix has exactly one entry 1 in each row and each column and 0's elsewhere. | ||
*A permutation matrix is nonsingular, and its determiant + or -. | *A permutation matrix is nonsingular, and its determiant + or -. | ||
| − | *Also permutation matrix A having the following properties <math>AA^ | + | *Also permutation matrix A having the following properties <math>AA^T=I</math>, where <math>A^T</math> is a transpose and I is the identity matrix. |
*Permutation matrices are orthogonal (hence, their inverse is their transpose: <math>P^{-1} = P^T</math>). | *Permutation matrices are orthogonal (hence, their inverse is their transpose: <math>P^{-1} = P^T</math>). | ||
*A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product. | *A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product. | ||
*In calci MATRIX("permutation",4) gives the permutation matrix of order 4. | *In calci MATRIX("permutation",4) gives the permutation matrix of order 4. | ||
Revision as of 12:50, 30 April 2015
MATRIX("PERMUTATION",order)
- is the size of the Permutation matrix.
Description
- This function returns the matrix Permutation matrix of order 3.
- A permutation matrix is a square binary matrix obtained by permuting the rows of an nxn identity matrix according to some permutation of the numbers 1 to n.
- This matrix has exactly one entry 1 in each row and each column and 0's elsewhere.
- A permutation matrix is nonsingular, and its determiant + or -.
- Also permutation matrix A having the following properties , where is a transpose and I is the identity matrix.
- Permutation matrices are orthogonal (hence, their inverse is their transpose: ).
- A permutation matrix allows to exchange rows or columns of another via the matrix-matrix product.
- In calci MATRIX("permutation",4) gives the permutation matrix of order 4.
 is the size of the Permutation matrix.
is the size of the Permutation matrix.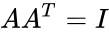 , where
, where 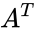 is a transpose and I is the identity matrix.
is a transpose and I is the identity matrix.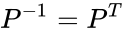 ).
).