Difference between revisions of "Manuals/calci/IDEMPOTENT"
Jump to navigation
Jump to search
| Line 8: | Line 8: | ||
*The properties of idempotent matrix is: | *The properties of idempotent matrix is: | ||
# <math>K^r=K</math> for r being a positive integer. | # <math>K^r=K</math> for r being a positive integer. | ||
| − | # I-K is idempotent. | + | # <math>I-K</math> is idempotent. |
# If <math>K_1</math> and <math>K_2</math> are idempotent matrices and <math>K_1K_2 =K_2K_1</math>. Then <math>K_1K_2</math> is idempotent. | # If <math>K_1</math> and <math>K_2</math> are idempotent matrices and <math>K_1K_2 =K_2K_1</math>. Then <math>K_1K_2</math> is idempotent. | ||
| + | |||
| + | ==Examples== | ||
| + | *1.MATRIXTYPE("idempotent",IM(19)) = true | ||
| + | *2.MATRIXTYPE([12,14],"idempotent") = false | ||
| + | *3.MATRIXTYPE(IM(5)|*|2,"idempotent") = false | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/IDENTITY| IDENTITY]] | ||
| + | *[[Manuals/calci/SYMMETRIC| SYMMETRIC]] | ||
| + | *[[Manuals/calci/PASCAL| PASCAL]] | ||
| + | *[[Manuals/calci/TRIANGULAR| TRIANGULAR]] | ||
| + | |||
| + | ==References== | ||
Revision as of 13:32, 5 May 2015
MATRIX("IDEMPOTENT",order)
- is the size of the Idempotent matrix.
Description
- This function is showing the idempotent matrix of order 3.
- An idempotent matrix is a matrix which, when multiplied by itself, is getting the same matrix.
- i.e.,A square matrix K is said to be idempotent if .
- The properties of idempotent matrix is:
- for r being a positive integer.
- is idempotent.
- If and are idempotent matrices and . Then is idempotent.
Examples
- 1.MATRIXTYPE("idempotent",IM(19)) = true
- 2.MATRIXTYPE([12,14],"idempotent") = false
- 3.MATRIXTYPE(IM(5)|*|2,"idempotent") = false
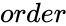 is the size of the Idempotent matrix.
is the size of the Idempotent matrix.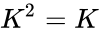 .
.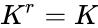 for r being a positive integer.
for r being a positive integer.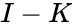 is idempotent.
is idempotent.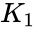 and
and  are idempotent matrices and
are idempotent matrices and 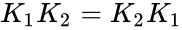 . Then
. Then 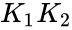 is idempotent.
is idempotent.