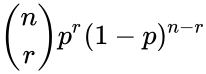Difference between revisions of "Manuals/calci/BINOMIALPROBABILITY"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:25px">'''BINOMIALPROBABILTY(NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)'''</div><br/> | <div style="font-size:25px">'''BINOMIALPROBABILTY(NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)'''</div><br/> | ||
| − | *<math> | + | *<math>Numberoftrials</math> is the trials occured. |
| + | *<math>NumberofSuccess</math> is the success occured. | ||
| + | |||
==Description== | ==Description== | ||
Revision as of 11:24, 12 May 2015
BINOMIALPROBABILTY(NumberOftrials,NumberOfSuccess,ProbabiltyOfSuccess)
- is the trials occured.
- is the success occured.
Description
- This function gives the probability value of the Binomial distribution.
- A binomial experiment has the following characteristics:
- 1.The experiment involves repeated trials.
- 2.Each trial has only two possible outcomes - a success or a failure.
- 3.The probability that a particular outcome will occur on any given trial is constant.
- 4.All of the trials in the experiment are independent.
- A binomial probability refers to the probability of getting EXACTLY r successes in a specific number of trials.
- The number of trials refers to the number of attempts in a binomial experiment.
- The number of trials is equal to the number of successes plus the number of failures.
- When computing a binomial probability, it is necessary to calculate and multiply three separate factors:
- 1. the number of ways to select exactly r successes,
- 2. the probability of success (p) raised to the r power,
- 3. the probability of failure (q) raised to the (n - r) power.
- The formula for Binomial probability is:
or
where n = number of trials,r = number of specific events you wish to obtain. p = probability that the event will occur, q = probability that the event will not occur.(q = 1 - p, the complement of the event)
Examples
- BINOMIALPROBABILTY(5,3,0.4)=0.23040000000000005
- BINOMIALPROBABILTY(10,4,0.25)=0.1459980010986328
- BINOMIALPROBABILTY(12,11,0.75)=0.12670540809631348
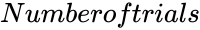 is the trials occured.
is the trials occured.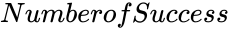 is the success occured.
is the success occured.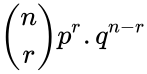 or
or