Units

How to specify units

Units are a unique, inherent and simple feature of the z^3 language.

Using units is simple and easy. For example:

a=1m;

indicates that a is now a variable containing the value of 1 meter. For more complex units we can enclose them in brackets as in 3(m/sec).

If a variable needs to be specified in specific units, simply use the <> operator. Such as: a<>(m/sec);

In z^3 language, <> is the unit conversion operator. Also, any arithmetic operator such as +, -, *, /, ^, % etc. should be enclosed within < and > to allow unit conversions to propagate through these operations. These conversion operations can be done on arrays as parameters also. Hence to add a meter to 2 centimeters, do the following: a=1m<+>2cm; and z^3 will give the answer: 102 cm.

Note, that this result now carries the units with it for further operations. For example: a=(1m<+>2cm)<^>3; gives the answer as 1061208 cm3.

To convert the current value of a variable to a different unit, simply use the <> operator: a<>cm;

Notice that if a already had a unit, it will be appropriately converted using the units. If it did not have units inherently, it will simply be given the units.

a=1

1

a<>cm;

1 cm.

a=1m;

1 m.

a<>cm;

100 cm.

In the second case, 1m is converted to 100cm.

Unit Prefixes

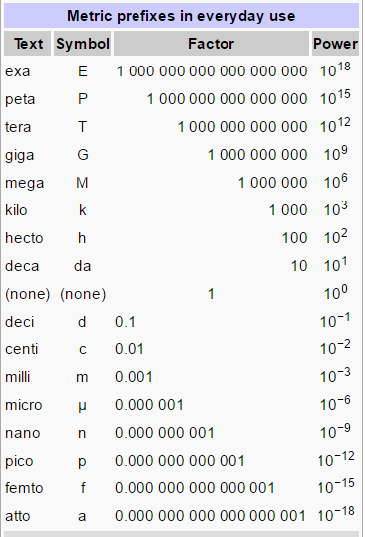
Similarly, scales such as milli, mega, etc. are supported using conventional SI units.

a=1m;

1 m.

a<>ym;

1.0000000000000001e+24 ym.

Here a now has the unit yoctometer.

Using uppercase Y, we get the answer in Yottameter.

a=1m;

1 m.

a<>Ym;

1.0000000000000001e-24 Ym.

These conversions of scale follow the SI unit prefix standards.

Conversion among Unit Systems

z^3 supports conversion among unit systems, such as SI Units and FPS systems.

For example:

a=1mi;

1 mi.

a<>km;

1.6093439999999999 km.

Notice that the mi (miles) unit of variable a is converted to km.

Units on Array of Values

Units work on variables as simple numerical values or as arrays.

Let us consider numbers 1 to 10.

a=1..10;

Then say this is in miles.

b=a<>(mi);

Convert to kilometers.

b<>km

Numeric	Units	UNITSOF
1mi	km	1.6093439999999999km
2mi	km	3.2186879999999998km
3mi	km	4.828031999999999km
4mi	km	6.4373759999999995km
5mi	km	8.046719999999999km
6mi	km	9.656063999999999km
7mi	km	11.265407999999999km
8mi	km	12.874751999999999km
9mi	km	14.484096km
10mi	km	16.093439999999998km

We can convert arrays of Unit values to converted values as in the following:

a=(1..10)<>℃;

b=a<>℉;

Numeric	Units	UNITSOF
1℃	degF	33.8℉
2℃	degF	35.6℉
3℃	degF	37.4℉
4℃	degF	39.2℉
5℃	degF	41℉
6℃	degF	42.8℉
7℃	degF	44.6℉
8℃	degF	46.4℉
9℃	degF	48.2℉
10℃	degF	50℉

Units inside functions

Units can be highly effective inside functions. These, along with constants, provide a fantastic way to express your logic beautifully.

Let us consider how we can write E=mc^2. E:=(m<>kg)<*>(SPEEDOFLIGHT()<^>2);

E(2kg)

gives: 179751035747363520kg.m2.s-2

Note the use of <*> and <^> for the operators in unit operations.

In case you wanted to give the output in Joules.

E(2kg)<>J

gives: 179751035747363520J

Let us add variables intermixing miles and kilometer.

a=1mi;

b=10km;

[a,b,(a<+>b)<>mi]

[a,b,(a<+>b)<>mi]

1mi

10km

7.21371192237334mi

10mi<>km

can convert miles to kilometers.

Units Aware Internal Functions

In most sytems, functions like SIN operate on radians. Most users are unaware of this, and get confused when they get SIN(90) to be something unexpected.

With z^3 unit aware functions, this is not an issue.

For example,

a=90deg; SIN(a)

will automatically convert the variable a into radians before calculations. To see the difference, try SIN(90) vs. SIN(90<>deg).

The answers given are: 0.8939966636005579 and 1.

Unit awareness is built into functions in z^3. (Note: Some functions are being transitioned).

Generation of Arrays with Units

rad2piby10

0㎭

0.6283185307179586㎭

1.2566370614359172㎭

1.8849555921538759㎭

2.5132741228718345㎭

3.141592653589793㎭

3.7699111843077517㎭

4.39822971502571㎭

5.026548245743669㎭

5.654866776461628㎭

6.283185307179586㎭

Note the results from rad2piby10 is automatically in radians.

Similarly array results using series in degrees are also marked with units of degrees.

deg110by10

0°

10°

20°

30°

40°

50°

60°

70°

80°

90°

100°

110°

(rad2piby10)<>rad<>deg

Numeric	Units	UNITSOF
0㎭	deg	0°
0.6283185307179586㎭	deg	36°
1.2566370614359172㎭	deg	72°
1.8849555921538759㎭	deg	108°
2.5132741228718345㎭	deg	144°
3.141592653589793㎭	deg	180°
3.7699111843077517㎭	deg	216°
4.39822971502571㎭	deg	252°
5.026548245743669㎭	deg	288°
5.654866776461628㎭	deg	324°
6.283185307179586㎭	deg	360°

shows the series in radians converted to degrees.

Currency Conversions

z^3 can automatically convert currencies.

b=(100$<+>3020¢);

gives the result

13020 cent.

b<>$;

gives

130.2 dollar.

With internal and external mappings to currency conversion dates, z^3 is able to do international currency conversions also.

(100..1000..100)<>USD<>INR

Numeric	Units	UNITSOF
100USD	INR	6680.820948336871INR
200USD	INR	13361.641896673742INR
300USD	INR	20042.462845010614INR
400USD	INR	26723.283793347484INR
500USD	INR	33404.10474168436INR
600USD	INR	40084.92569002123INR
700USD	INR	46765.7466383581INR
800USD	INR	53446.56758669497INR
900USD	INR	60127.388535031845INR
1000USD	INR	66808.20948336872INR

We can override internal conversion rates by using SETCONVERSION.

SETCONVERSION(1<>euro,1<>dollar,1.1)

PRINTCONVERSION();

can give the recently set conversion rates.

1<>€<>$

gives 1 euro to convert to 1$.

SETCONVERSION(1$,1€,0.9);

shows the following on PRINTCONVERSION(): {

  dollar:euro: 0.9,
  euro:dollar: 1.1111111111111112

}

Adding currencies is demonstrated further below:

(100$<+>300¢<+>30¢)<>$

gives:

103.3 dollar.

Array Unit Normalization

If an array holds a set of values from varied units, UNITIFY can convert all of them to the same units.

UNITIFY([1cm,2m,3cm])

will give: 1cm 200cm 3cm

Likewise: SUM(UNITIFY([1m,2m,3mm]))

will give the answer:

3.003 m.

SUM(UNITIFY([1m,2m,3mm]))<>cm

will give answer in cm :

300.3cm

PMT(4%,12,1000$,1200¢,0)

gives the result as:

-107.35079875828919 dollar.

since PMT is a unit aware function.

A gallon is converted to liter below.

1gal<>l

3.786235392 l.

A liter is converted to oz. below:

1<>l<>oz

33.806667242732274 oz.

Shown below are conversions to micro liters.

(1..10)<>l<>ul

Numeric	Units	UNITSOF
1l	ul	999999.9999999999ul
2l	ul	1999999.9999999998ul
3l	ul	2999999.9999999995ul
4l	ul	3999999.9999999995ul
5l	ul	4999999.999999999ul
6l	ul	5999999.999999999ul
7l	ul	6999999.999999999ul
8l	ul	7999999.999999999ul
9l	ul	8999999.999999998ul
10l	ul	9999999.999999998ul

MORE

(1..100)<>l<>ul 1Pa<>atm

E:=(m<>kg)<*>(SPEEDOFLIGHT()<^>2); b=E(2g); ConvertToUnitOfNature(b,"energy")

1m<>>1cm;

[1m,2m]<>>[1cm,200cm];

[1m,2m]<>=>[1cm,200cm];

[1m,2m]<<>[1cm,200cm];

[1m,2m]<<>[1cm,200cm];

[1m,2m]<==>[1cm,200cm];

[1m,2m]<!=>[1cm,200cm];

[1m,2m]<<=>[1cm,199.99cm];

[1m,2m]<<=>[1cm,200.01cm];

((1..10)<>m)<>>3m;

((0.1..10)<>m)<>>30cm

CONSTANT("G") CONSTANT("G")<*>1kg<*>110kg</>(6000m<^>2) // did not work.

(CONSTANT("G")<*>1kg<*>110kg)</>((6000m)<^>2) // how to bracket the units to be inside and ignore < etc? // ## can be used to name variables with spaces in them. // the actual variable is named by removing the spaces. // otherwise it goes into code as it is. ##weight of zone=3m; ++(##weight of zone);

##weight of zone=3m; a=3.4mm<+>(##weight of zone);

//%G is gravitational constant GF:=%G*m1*m2/r^2; GF(1,2,300)

v:=u+%g*t; // this uses %g as default g value v(1,2)

%planck %boltzmann; %planck length;

PRINTCONVERSIONS() CONSTANTS() CONVERT()

A¹=34; A=[23,4,5,5]; /* no array indexing on subscript yet. Will decide on that later. */ A¹=[23,4,5,5] A¹[2]

a=%gravit; b=30<*>a

a=%gravit; b=(1..10)<*>a

E:=m<>kg<*>%c<^>2; E(1000kg) E(1000kg<>lbm) // - will gave same result as 1000kg E(1000lbm) //lbm is used for units of lb mass.

// %G<*>1kg<*>110kg(6000m<^>2) // %G<*>1kg<*>110kg((6000m)<^>2) // -did not work. Said 7.34149141e-9Nm3UNITPOWERUNITSOF %G<*>1kg<*>110kg<*>((6000m)<^>2)

%G<*>1kg<*>110kg</>((6000m)<^>2)

// make this work. 1..100 @> x.txt; // send output to a <@ x.txt; // read input from a;

1.3J<>GeV 1.3J<>eV

1J<>l.atm; // 0.0098692latm 1J<>(l.atm-1) // this should fail. and will keep original units. maybe safer. 1m2<>in2 1m²<>in²

10m2<>are 1m2<>are

100m2<>acre

E:=m<>kg<*>%c<^>2; b=E(1000kg)<>J

   c=b<>eV;

[b,c]

1..100.$("[SIN(x),COS(x),TAN(x)]") 1..100.$([SIN,COS,TAN]) worked. 1..100.$("[x,x^2,x^3,x^4,x^3+x^4,SIN(x)]") works 1..100.$("[SIN(x),COS(x),TAN(x)]") 1..100.$([SIN,COS,TAN]) x=SERIESOF("1/x",9,10) //this is to from in parameter sequence. x=SERIESOF("1/x",19,10) SERIESOF("1/x",10,5) x=SERIESOF "1/LOG(x,2)" 100 1 x=SERIESOF "1/log2x" 100 91 //removed: 1..10.$_([+,-]) 1..10.$_([SUM,MINUS]) //removed: 1..10.$_|+| EXPOF(5) [SIN,COS]@[1..100] 1..10.$_("+") 1..10.$_("+") 1..10@["+"] 1..10@"+"

(1..100)<>m<+>10cm

MAGICSQUARE(3).$$(SUM) MAGICSQUARE(3).$$$(SUM) MAGICSQUARE(3).$_(SUM)

a=1m<>mm<+>400km 1m<>eor // should give nothing as there is no such conversion. (((1..100)<>m)<^>2)<>are

(1..1000)<>$ (((1..100)<>m)<^>2)<>km2 // why chinese headers here?

(1..100)m<>cm

F=%G<*>100kg<*>10g</>((100km)<^>2);

1.3J<>GeV //check this

velocity=3<>(m/sec); time=1hr; velocity<*>time;

1(g.m)<>(mg.cm)

a=LAZYRANGE(1,100) a(1..100) // generate numbers in the range at that interval, without having to generate the array ahead of time. Useful in things like INTEGRALS etc. a() a=LAZYOBJECT(1,100,1000) // can even take a(0.1); a.islazyrange()

1(kg.m2s-2)<>(N.m) 1(kg.m2s-2)<>J 1(kg.m2s-2)<>(N) // also should work as we want to get rid of the /s here in this case. 1(kg.m2s-2)<>(N.m2) // should fail. 1(kg.m2s-2)<>(J/s) // should fail. 1(kg.m2s-3)<>(J/s) 1(kg.m2.s)<>(J/s) // should this fail? it works now.

12(g.m-1/s)<>(g.cm) // should fail. 12(g.m)<>(g.mm) // should not fail. 12(g.m)<>(g.cm) // should not fail.

12(g.m)<>(g.s) // should fail. original should be returned. 12(g.m)<>(g.mm) 12(g.m)<>(g.s) 12(g.m-1)<>(g.mm-1) 12(g.m-1/s)<>(g.cm-1) // converts, but this is ok, since /s on left sometimes we want to get rid off for some reason for using it on another calculation. Say N/s but you only want to use the N on it. 1(kg.m2/s2)<>e // how to make this conversion?

1(kg.m2/s2)<>J<>e

1.3(kg.m2/s2)<>Jo // would fail and original will be kept.

(((1..100)<>m)<^>2)<>are (1..100)<>are [1cm2,2m2]<>are %pi*34; %e; %avo;

q=1(mol/s); heat=%avo<*>q;

1Pa<>atm 1atm<>psi 1atm<>hPa

a=1<>(kg/m.s-2)<>Pa<>torr 1J<>BTU 1ly<>m 10ly<>m<>km

1atm<>inHg<>mmHg

1atm<+>1bar (1atm<+>1bar)<>atm 1km<>m<>lightyear

1lightyear<>km

1lightyear<>pc

1m<>ly

1km<>ly //seemed off. this is possibly correct. (1km<+>1ly)<>km

1Å<>km

1Å<>m

(1..100)<>AU<>m

1degree<>arcminute

1Tsec<>sec

1(m/s)<>(km/hr) 1(km/s)<>(km/hr)

1(cal/mn)<>(J/sec) // d

1(kg/m3)<>(slug.ft-3)

2(rad/sec)<>rpm // did not convert. not sure why.

(1..100)<>USD<>EUR

SUPPORTEDUNITS()

1nibble<>bit 102400000000bit<>MB 1kB<>MB // seems wrong. 1kB<>Mb 1(kb)<>(bit) Pi<>(rad/sec)<>rpm 1(rad/sec)<>rpm 1(rad/mn)<>rpm (1(rad/mn)<>rpm)*2*Pi // should give 1. 1(rotation/mn)<>rpm 1(cycle/mn)<>(rad/mn)

1(cycle/mn)<>rpm

60rad<>deg 60rad<>deg<>rotation

1MB<>kB 1B<>kB 1MB<>B 1kB<>B

a=1(kg/m/s-2/t3) a=1(kg/m/s-2/t3) a=1(kg/m/s-2/t3) a=1(kg/m/s-2/t3) a=1<>(kg/m.s-2) // this worked though.

1(kg/m3)<>(slug/ft^3) // will not work due to ^. 1(kg/m3)<>(slug/ft3) //works 1(kg/m3)<>(slug.ft-3) //works

1(s-1)<>Hz 1(mn-1)<>Hz

velocity=3<>(m/s); time=1hr; velocity<*>time;

(((1..100)<>m)<^>2)<>acre

((1..100)<>m)<^>2