Difference between revisions of "Manuals/calci/ACKERMANN"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
*All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. | *All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. | ||
*Its arguments are never negative and it always terminates. | *Its arguments are never negative and it always terminates. | ||
| − | * | + | *The two-argument Ackermann–Péter function, is defined as follows: |
<math>A(m,n) = \begin{cases} n+1 \mbox {if} m=0 \\ | <math>A(m,n) = \begin{cases} n+1 \mbox {if} m=0 \\ | ||
A(m-1,1) & \mbox {if} m>0 and n=0 \\ | A(m-1,1) & \mbox {if} m>0 and n=0 \\ | ||
A(m-1,A(m,n-1))& \mbox {if} m>0 and n>0 | A(m-1,A(m,n-1))& \mbox {if} m>0 and n>0 | ||
| − | \end{cases} </math> | + | \end{cases} </math>\\ |
| − | for nonnegative integers m and n. | + | for nonnegative integers m and n. |
*Its value grows rapidly, even for small inputs. | *Its value grows rapidly, even for small inputs. | ||
| + | |||
| + | ==Example== | ||
Revision as of 13:10, 21 September 2016
ACKERMANN(m,n)
- and are the positive integers.
Description
- The Ackermann function is a classic example of a recursive function, notable especially because it is not a primitive recursive function.
- All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive.
- Its arguments are never negative and it always terminates.
- The two-argument Ackermann–Péter function, is defined as follows:
\\
for nonnegative integers m and n.
- Its value grows rapidly, even for small inputs.
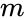 and
and  are the positive integers.
are the positive integers. \\
\\