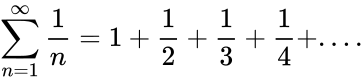Difference between revisions of "Manuals/calci/HARMONICSERIES"
Jump to navigation
Jump to search
| Line 11: | Line 11: | ||
*Every term of the series after the first is the harmonic mean of the neighboring terms. | *Every term of the series after the first is the harmonic mean of the neighboring terms. | ||
*The phrase harmonic mean likewise derives from music. | *The phrase harmonic mean likewise derives from music. | ||
| + | |||
| + | ==Examples== | ||
| + | #HARMONICSERIES(3,10,4) = 0.3333333333333333 | ||
| + | #HARMONICSERIES(189,20,18) = 9.947368421052632 | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/SUM | SUM]] | ||
| + | *[[Manuals/calci/AVERAGE | AVERAGE ]] | ||
| + | *[[Manuals/calci/AVERAGEA | AVERAGEA ]] | ||
Revision as of 14:40, 28 November 2016
HARMONICSERIES (Start,Numbers,OnlyNth)
- are any positive integer .
- is the number of the series.
- is the Nth term of the series.
Description
- This sfunction displays the Harmonic series of the numbers.
- A series is an expression with an infinite number of terms, like this:
- This is the divergent infinite series.
- In HARMONICSERIES(Start,Numbers,OnlyNth),Start is the beginning number of the series, Numbers is number of the number in the series and OnlyNth is the nth term of the Harmonic Series.
- Every term of the series after the first is the harmonic mean of the neighboring terms.
- The phrase harmonic mean likewise derives from music.
Examples
- HARMONICSERIES(3,10,4) = 0.3333333333333333
- HARMONICSERIES(189,20,18) = 9.947368421052632
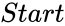 are any positive integer .
are any positive integer .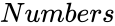 is the number of the series.
is the number of the series.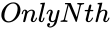 is the Nth term of the series.
is the Nth term of the series.