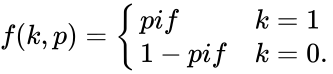Difference between revisions of "Manuals/calci/BERNOULLIDISTRIBUTED"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
*The Bernoulli distribution is defined by:<math>f(x)=p^x(1-p)^{1-x} </math> for x={0,1}, where p is the probability that a particular event will occur. | *The Bernoulli distribution is defined by:<math>f(x)=p^x(1-p)^{1-x} </math> for x={0,1}, where p is the probability that a particular event will occur. | ||
*The probability mass function is : | *The probability mass function is : | ||
| − | <math>f(k,p) = \begin{cases}p | + | <math>f(k,p) = \begin{cases} p if & k=1\\ |
| − | 1-p | + | 1-p if & k=0. \\ |
\end{cases}</math> | \end{cases}</math> | ||
*This function will give the result as error when | *This function will give the result as error when | ||
| − | 1. Any one of the argument is | + | 1. Any one of the argument is non numeric. |
2. The value of p<0 or p>1. | 2. The value of p<0 or p>1. | ||
| + | |||
| + | |||
| + | \begin{cases} | ||
| + | 3x + 5y + z &= 1 \\ | ||
| + | 7x - 2y + 4z &= 2 \\ | ||
| + | -6x + 3y + 2z &= 3 | ||
| + | \end{cases} | ||
Revision as of 14:00, 7 December 2016
BERNOULLIDISTRIBUTED (Numbers,Probability)
- is the number of variables.
- is the value range from 0 to 1.
Description
- This function gives the value of the Bernoulli distribution.
- It is a discrete probability distribution.
- Bernoulli distribution is the theoretical distribution of the number of successes in a finite set of independent trials with a constant probability of success.
- The Bernoulli distribution is simply BINOM(1,P).
- This distribution best describes all situations where a trial is made resulting in either success or failure, such as when tossing a coin, or when modeling the success or failure.
- In , represents the number of variables.
- is the probability value.
- The vaule is ranges from 0 to 1.
- The Bernoulli distribution is defined by: for x={0,1}, where p is the probability that a particular event will occur.
- The probability mass function is :
- This function will give the result as error when
1. Any one of the argument is non numeric. 2. The value of p<0 or p>1.
\begin{cases}
3x + 5y + z &= 1 \\
7x - 2y + 4z &= 2 \\
-6x + 3y + 2z &= 3
\end{cases}
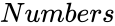 is the number of variables.
is the number of variables.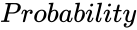 is the value range from 0 to 1.
is the value range from 0 to 1. ,
,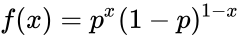 for x={0,1}, where p is the probability that a particular event will occur.
for x={0,1}, where p is the probability that a particular event will occur.