Difference between revisions of "Manuals/calci/CARTESIANPRODUCT"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y. | *The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y. | ||
*In <math>CARTESIANPRODUCT(GivenSet1,GivenSet2)</math>,<math>Givenset1</math> and <math>Givenset2</math> are two set of real numbers with a pair of numbers. | *In <math>CARTESIANPRODUCT(GivenSet1,GivenSet2)</math>,<math>Givenset1</math> and <math>Givenset2</math> are two set of real numbers with a pair of numbers. | ||
| − | *Consider two sets A and B. | + | *Consider two sets <math>\llcorner A </math> and <math>\llcorner B </math>. |
| − | *The Cartesian product of A and B are denoted by | + | *The Cartesian product of <math>\llcorner A </math> and <math>\llcorner B </math> are denoted by <math>\llcorner AxB </math> is the set of all ordered pairs <math>\llcorner (a,b) </math> such that <math>a \in A</math> and <math>b \in B</math>. |
<math>\llcorner A </math> | <math>\llcorner A </math> | ||
| + | |||
==References== | ==References== | ||
[http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | [http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | ||
Revision as of 19:16, 21 December 2016
CARTESIANPRODUCT (GivenSet1,GivenSet2)
- and are the set of numbers to find product.
Description
- This function shows the Cartesian product of two sets.
- Cartesian product is the product of two sets.
- The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y.
- In , and are two set of real numbers with a pair of numbers.
- Consider two sets and .
- The Cartesian product of and are denoted by is the set of all ordered pairs such that and .
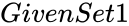 and
and 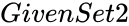 are the set of numbers to find product.
are the set of numbers to find product.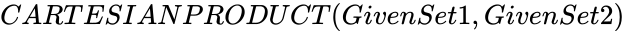 ,
,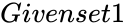 and
and 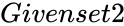 are two set of real numbers with a pair of numbers.
are two set of real numbers with a pair of numbers.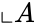 and
and 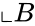 .
.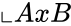 is the set of all ordered pairs
is the set of all ordered pairs 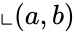 such that
such that 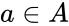 and
and 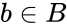 .
.