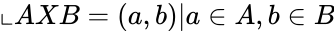Difference between revisions of "Manuals/calci/CARTESIANPRODUCT"
Jump to navigation
Jump to search
| Line 9: | Line 9: | ||
*Consider two sets <math>\llcorner A </math> and <math>\llcorner B </math>. | *Consider two sets <math>\llcorner A </math> and <math>\llcorner B </math>. | ||
*The Cartesian product of <math>\llcorner A </math> and <math>\llcorner B </math> are denoted by <math>\llcorner AXB </math> is the set of all ordered pairs <math>\llcorner (a,b) </math> such that <math>a \in A</math> and <math>b \in B</math>. | *The Cartesian product of <math>\llcorner A </math> and <math>\llcorner B </math> are denoted by <math>\llcorner AXB </math> is the set of all ordered pairs <math>\llcorner (a,b) </math> such that <math>a \in A</math> and <math>b \in B</math>. | ||
| − | <math>\llcorner A </math> | + | <math>\llcorner AXB ={(a,b)|a \in A,b \in B} </math> |
==References== | ==References== | ||
[http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | [http://ndp.jct.ac.il/tutorials/discrete/node28.html Cartesian Product] | ||
Revision as of 18:19, 21 December 2016
CARTESIANPRODUCT (GivenSet1,GivenSet2)
- and are the set of numbers to find product.
Description
- This function shows the Cartesian product of two sets.
- Cartesian product is the product of two sets.
- The product of set X and set Y is the set that contains all ordered pairs ( x, y ) for which x belongs to X and y belongs to Y.
- In , and are two set of real numbers with a pair of numbers.
- Consider two sets and .
- The Cartesian product of and are denoted by is the set of all ordered pairs such that and .
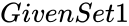 and
and 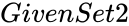 are the set of numbers to find product.
are the set of numbers to find product.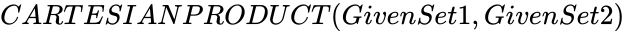 ,
,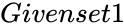 and
and 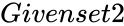 are two set of real numbers with a pair of numbers.
are two set of real numbers with a pair of numbers.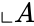 and
and 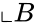 .
.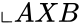 is the set of all ordered pairs
is the set of all ordered pairs 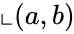 such that
such that 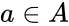 and
and 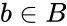 .
.