Difference between revisions of "Manuals/calci/CROSSPRODUCT"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
*The cross product is defined in three dimensional space and it is denoted by axb. | *The cross product is defined in three dimensional space and it is denoted by axb. | ||
*In CROSSPRODUCT (a,b), a and b are any two positive real numbers. | *In CROSSPRODUCT (a,b), a and b are any two positive real numbers. | ||
| − | *We can calculate the Cross Product this way: | + | *We can calculate the Cross Product this way: <math>a×b</math> = <math>\mid a\mid</math>.<math> \mid b\mid</math><math> sin(\theta) n</math> |
| − | <math> | ||
*<math>\mid a\mid</math> is the magnitude (length) of vector a | *<math>\mid a\mid</math> is the magnitude (length) of vector a | ||
*<math>\mid b</math> is the magnitude (length) of vector b | *<math>\mid b</math> is the magnitude (length) of vector b | ||
*<math>\theta</math> is the angle between a and b | *<math>\theta</math> is the angle between a and b | ||
*n is the unit vector at right angles to both a and b | *n is the unit vector at right angles to both a and b | ||
Revision as of 17:19, 28 December 2016
CROSSPRODUCT (a,b)
- and are any real numbers.
Description
- This function shows the Cross product of two numbers.
- Cross product is also called Vector product.
- The cross product is defined in three dimensional space and it is denoted by axb.
- In CROSSPRODUCT (a,b), a and b are any two positive real numbers.
- We can calculate the Cross Product this way: Failed to parse (syntax error): {\displaystyle a×b} = .
- is the magnitude (length) of vector a
- is the magnitude (length) of vector b
- is the angle between a and b
- n is the unit vector at right angles to both a and b
 and
and  are any real numbers.
are any real numbers.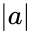 .
.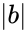
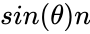
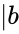 is the magnitude (length) of vector b
is the magnitude (length) of vector b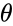 is the angle between a and b
is the angle between a and b