Difference between revisions of "Manuals/calci/DYADIC"
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
A_y \\ | A_y \\ | ||
A_z | A_z | ||
| − | \end{pmatrix}</math><math> (B_x B_y B_Z)</math>method | + | \end{pmatrix}</math><math> (B_x B_y B_Z)</math>=\begin{pmatrix} |
| + | A_xB_x & A_xB_y & A_xB_z \\ | ||
| + | A_yB_x & A_yB_y & A_yB_z \\ | ||
| + | A_z B_x &A_zB_y & A_zB_z | ||
| + | \end{pmatrix}method | ||
*The direct product is non-commutative (AB 6D BA).A few vector product identities are of interest | *The direct product is non-commutative (AB 6D BA).A few vector product identities are of interest | ||
Revision as of 14:35, 3 March 2017
DYADIC(a,b)
OR VECTORDIRECTPRODUCT (a,b)
- and any two set of values.
Description
- This function shows the Vector Direct product.
- The third type of vector multiplication is called the direct product, and is written AB.
- In , and are the two vectors.
- Multiplying one vector by another under the direct product gives a tensor result.
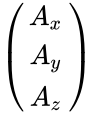
- The rectangular components of the direct product may be found by matrix multiplication: one multiplies the column vector A by the transpose of B, which gives a 3X3 matrix:
= =\begin{pmatrix} A_xB_x & A_xB_y & A_xB_z \\ A_yB_x & A_yB_y & A_yB_z \\ A_z B_x &A_zB_y & A_zB_z \end{pmatrix}method
- The direct product is non-commutative (AB 6D BA).A few vector product identities are of interest
 and
and 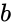 any two set of values.
any two set of values.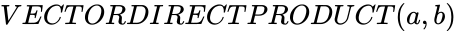 ,
, 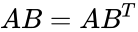 =
=
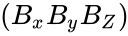 =\begin{pmatrix}
A_xB_x & A_xB_y & A_xB_z \\
A_yB_x & A_yB_y & A_yB_z \\
A_z B_x &A_zB_y & A_zB_z
\end{pmatrix}method
=\begin{pmatrix}
A_xB_x & A_xB_y & A_xB_z \\
A_yB_x & A_yB_y & A_yB_z \\
A_z B_x &A_zB_y & A_zB_z
\end{pmatrix}method