Difference between revisions of "Manuals/calci/NORMDIST"
Jump to navigation
Jump to search
| Line 1: | Line 1: | ||
<div style="font-size:30px">'''NORMDIST(x,m,sd,cu)'''</div><br/> | <div style="font-size:30px">'''NORMDIST(x,m,sd,cu)'''</div><br/> | ||
| − | *<math> | + | NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy) |
| + | |||
| + | *<math>Number</math> is the value. | ||
| + | *<math>Mean</math> is the mean. | ||
| + | *<math>StandardDeviation</math> is the standard deviation | ||
| + | *<math>Cumulative</math> is the logical value like TRUE or FALSE. | ||
| + | **NORMDIST(),returns the normal cumulative distribution | ||
==Description== | ==Description== | ||
| Line 6: | Line 12: | ||
*Normal Distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph. | *Normal Distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph. | ||
*This distribution is the Continuous Probability Distribution.It is also called Gaussian Distribution. | *This distribution is the Continuous Probability Distribution.It is also called Gaussian Distribution. | ||
| − | *In <math> NORMDIST( | + | *In <math>NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)</math>), <math>Number</math> is the value of the function, <math>Mean</math> is the Arithmetic Mean of the distribution, <math>StandardDeviation</math> is the Standard Deviation of the distribution and <math>Cumulative</math> is the Logical Value that indicating the form of the function. |
| − | *Suppose <math> | + | *Suppose <math>Cumulative</math> is TRUE, this function gives the Cumulative Distribution, and it is FALSE, this function gives the Probability Mass Function. |
*The equation for the Normal Distribution is: | *The equation for the Normal Distribution is: | ||
<math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^{-\left({\tfrac{(x-\mu)^2}{2\sigma^2}}\right)}</math> | <math> f(x,\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}.e^{-\left({\tfrac{(x-\mu)^2}{2\sigma^2}}\right)}</math> | ||
where <math>\mu</math> is the Mean of the distribution, <math>\sigma</math> is the Standard Deviation of the distribution. | where <math>\mu</math> is the Mean of the distribution, <math>\sigma</math> is the Standard Deviation of the distribution. | ||
*In this formula, suppose <math>\mu</math> = 0 and <math>\sigma</math>= 1, then the distribution is called the Standard Normal Distribution or the Unit Normal Distribution. | *In this formula, suppose <math>\mu</math> = 0 and <math>\sigma</math>= 1, then the distribution is called the Standard Normal Distribution or the Unit Normal Distribution. | ||
| − | This function will return the result as error when any one of the argument is non-numeric and <math> | + | This function will return the result as error when any one of the argument is non-numeric and <math>StandardDeviation<=0</math>. |
| − | *when <math> | + | *when <math>Cumulative</math> is TRUE , this formula is the integral from <math>-\infinity</math> to <math>Number</math> and <math>Cumulative</math> is FALSE , we can use the same formula. |
==Examples== | ==Examples== | ||
Revision as of 16:49, 14 June 2018
NORMDIST(x,m,sd,cu)
NORMDIST (Number,Mean,StandardDeviation,Cumulative,accuracy)
- is the value.
- is the mean.
- is the standard deviation
- is the logical value like TRUE or FALSE.
- NORMDIST(),returns the normal cumulative distribution
Description
- This function gives the Normal Distribution for the particular Mean and Standard Deviation.
- Normal Distribution is the function that represents the distribution of many random variables as a symmetrical bell-shaped graph.
- This distribution is the Continuous Probability Distribution.It is also called Gaussian Distribution.
- In ), is the value of the function, is the Arithmetic Mean of the distribution, is the Standard Deviation of the distribution and is the Logical Value that indicating the form of the function.
- Suppose is TRUE, this function gives the Cumulative Distribution, and it is FALSE, this function gives the Probability Mass Function.
- The equation for the Normal Distribution is:
where is the Mean of the distribution, is the Standard Deviation of the distribution.
- In this formula, suppose = 0 and = 1, then the distribution is called the Standard Normal Distribution or the Unit Normal Distribution.
This function will return the result as error when any one of the argument is non-numeric and .
- when is TRUE , this formula is the integral from Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\infinity} to and is FALSE , we can use the same formula.
Examples
- =NORMDIST(37,29,2.1,FALSE) = 0.000134075
- =NORMDIST(37,29,2.1,TRUE) = 0.99993041384
- =NORMDIST(10.75,17.4,3.2,TRUE) = 0.01884908749
- =NORMDIST(10.75,17.4,3.2,FALSE) = 0.014387563
Related Videos
See Also
References
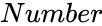 is the value.
is the value.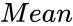 is the mean.
is the mean.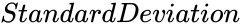 is the standard deviation
is the standard deviation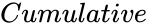 is the logical value like TRUE or FALSE.
is the logical value like TRUE or FALSE.
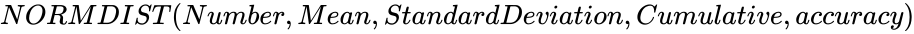 ),
), 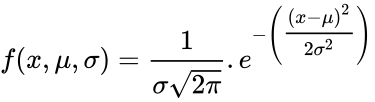
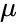 is the Mean of the distribution,
is the Mean of the distribution, 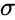 is the Standard Deviation of the distribution.
is the Standard Deviation of the distribution.
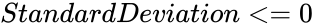 .
.