Difference between revisions of "Manuals/calci/SQRTPI"

Revision as of 15:33, 3 July 2018

SQRTPI(Multiplier)

This function gives the square root of $(pi*n)$ .
The $pi$ is a mathematical constant with a value approximate to 3.14159.
In $SQRTPI(Multiplier)$ , $Multiplier$ is the number by which $pi$ is multiplied. When we are omitting the value of $Multiplier$ , then it will consider the value $Multiplier=1$ .
$PI()$ is denoted by the Greek letter $\pi$ .
$\pi$ is a transcendental number and irrational number.
Being an irrational number, $\pi$ cannot be expressed exactly as a ratio of any two integers, but we can express as the fraction 22/7 is approximate to the $\pi$ value, also no fraction can be its exact value.

     This function will give the result as error when  $n<0$ .

@@ Line 1: / Line 1: @@
-<div style="font-size:30px">'''SQRTPI(n)'''</div><br/>
+<div style="font-size:30px">'''SQRTPI(Multiplier)'''</div><br/>
-*<math>n </math>  is the number.
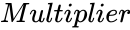+*<math>Multiplier</math>  is any number.
+**SQRTPI(), returns the square root of (number * pi)
 ==Description==
 *This function gives the square root of <math>(pi*n)</math>.
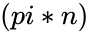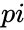 *The <math> pi</math> is a mathematical constant with a value approximate to 3.14159.
-*In <math> SQRTPI(n)</math>, <math>n</math> is the number by which <math> p </math> is multiplied. When we are omitting the value of <math> n</math>, then it will consider the value <math>n=1</math>.
+*In <math> SQRTPI(Multiplier)</math>, <math>Multiplier</math> is the number by which <math> pi </math> is multiplied. When we are omitting the value of <math> Multiplier</math>, then it will consider the value <math>Multiplier=1</math>.
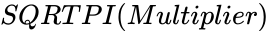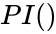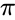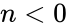 *<math> PI()</math> is denoted by the Greek letter <math> \pi</math>.
 *<math> \pi </math> is a transcendental number and irrational number.