Difference between revisions of "Manuals/calci/MCORREL"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''MCORREL (ArrayOfArrays) '''</div><br/> *<math>ArrayOfArrays</math> is set of values. ==Description== *This function is showing the result for m...") |
|||
| Line 8: | Line 8: | ||
*It is multiple if there is one variable on one side and a set of variables on the other side. | *It is multiple if there is one variable on one side and a set of variables on the other side. | ||
*If we have a series of <math>n</math> measurements of <math>X</math> and <math>Y</math> written as <math>x_i</math> and <math>y_i</math> where <math>i = 1, 2,...n</math> then the Sample Correlation Coefficient is: | *If we have a series of <math>n</math> measurements of <math>X</math> and <math>Y</math> written as <math>x_i</math> and <math>y_i</math> where <math>i = 1, 2,...n</math> then the Sample Correlation Coefficient is: | ||
| − | + | <math>CORREL(X,Y)= r_{xy}= \frac{\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)}{\sqrt{ \sum_{i=1}^n (x_i-\bar x)^2 \sum_{i=1}^n (y_i-\bar y)^2}}</math> | |
*<math>\bar x</math> and <math>\bar y</math> are the sample means of <math>X</math> and <math>Y</math>. | *<math>\bar x</math> and <math>\bar y</math> are the sample means of <math>X</math> and <math>Y</math>. | ||
*The above formula is used for simple correlation. | *The above formula is used for simple correlation. | ||
| Line 21: | Line 21: | ||
2.<math>Array of Arrays </math>is empty | 2.<math>Array of Arrays </math>is empty | ||
3.The denominator value is zero. | 3.The denominator value is zero. | ||
| + | <math>\sqrt{\frac{r_{xz}^2+r_{yz}^2-2 r_{xz} r_{yz} r_{xy}}{1-r_{xy}^2}</math> | ||
==Examples== | ==Examples== | ||
Revision as of 16:59, 5 July 2017
MCORREL (ArrayOfArrays)
- is set of values.
Description
- This function is showing the result for multiple correlation.
- In , are set of values.
- Correlation is a statistical technique which shows the relation of strongly paired variables.When one variable is related to a number of other variables, the correlation is not simple.
- It is multiple if there is one variable on one side and a set of variables on the other side.
- If we have a series of measurements of and written as and where then the Sample Correlation Coefficient is:
- and are the sample means of and .
- The above formula is used for simple correlation.
- Now consider the variables x,y and z we define the multiple correlation as:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{zxy}=\sqrt{\frac{r_{xz}^2+r_{yz}^2-2 r_{xz} r_{yz} r_{xy}}{1-r_{xy}^2}}
- is the correlation of x and y.
- is the correlation of y and z.
- is the correlation of z and x.
- Here x and y are viewed as the independent variables and z is the dependent variable.
- This function will give the result as error when
1. are non-numeric or different number of data points. 2.is empty 3.The denominator value is zero. Failed to parse (syntax error): {\displaystyle \sqrt{\frac{r_{xz}^2+r_{yz}^2-2 r_{xz} r_{yz} r_{xy}}{1-r_{xy}^2}}
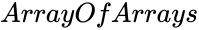 is set of values.
is set of values.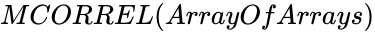 ,
,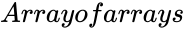 are set of values.
are set of values. measurements of
measurements of 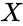 and
and 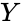 written as
written as 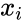 and
and 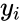 where
where 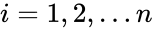 then the Sample Correlation Coefficient is:
then the Sample Correlation Coefficient is: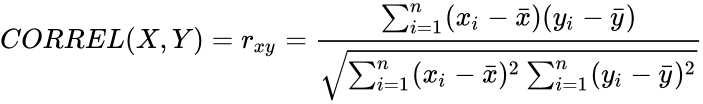
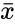 and
and 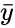 are the sample means of
are the sample means of 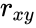 is the correlation of x and y.
is the correlation of x and y. is the correlation of y and z.
is the correlation of y and z. is the correlation of z and x.
is the correlation of z and x.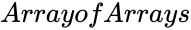 are non-numeric or different number of data points.
2.
are non-numeric or different number of data points.
2.