Difference between revisions of "Manuals/calci/QRDECOMPOSITION"
Jump to navigation
Jump to search
| Line 39: | Line 39: | ||
5.3446973501217775e-17 0 1.7054560140922779 | 5.3446973501217775e-17 0 1.7054560140922779 | ||
|} | |} | ||
| + | |||
| + | ==See Also== | ||
| + | *[[Manuals/calci/LUDECOMPOSITION| LUDECOMPOSITION]] | ||
| + | *[[Manuals/calci/CHOLESKYFACTORIZATION| CHOLESKYFACTORIZATION]] | ||
| + | *[[Manuals/calci/CONFERENCE| CONFERENCE]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | *[https://en.wikipedia.org/wiki/LU_decomposition LU Decomposition] | ||
| + | |||
| + | *[[Z_API_Functions | List of Main Z Functions]] | ||
| + | |||
| + | *[[ Z3 | Z3 home ]] | ||
Revision as of 15:54, 12 July 2017
QRDECOMPOSITION (Matrix)
- is the set of values.
Description
- This function gives the value of QR Decomposition.
- In , is any matrix.
- QR Decomposition is also called QR Factorization.
- QR Decomposition is defined by the product of Orthogonal matrix and Upper Triangular matrix.
- Consider any square matrix A may be decomposed as ,where stands for orthogonal matrix and stands for Upper Triangular matrix.
- An orthogonal matrix should satisfy ,where is identity or Unitary matrix.
- is the transpose matrix of Q.
- If the given matrix A is non singular, then this factorization is unique.
- Gram-Schmidt process is one of the process of computing decomposition in QR Decomposition method.
Examples
1. QRDECOMPOSITION([[2,6],[10,-15]])
-0.19611613513818393 -0.9805806756909202 |
-0.9805806756909202 0.19611613513818393 |
-10.19803902718557 13.5320133245347 |
-1.1102230246251565e-15 -8.825226081218279 |
2. QRDECOMPOSITION([[3,8,-5],[4,-6.3,9],[2,5,-1]])
-0.5570860145311556 0.631547425332445 -0.5392615524675877 |
-0.7427813527082074 -0.669329688618384 -0.01654176541311622 | -0.3713906763541037 0.3913382392381005 0.841975859527614 |
| -5.385164807134504 -1.634118975958056 -3.528211425363985 |
-2.1551618871879059e-16 11.22584763714588 -9.573042563465782 |
5.3446973501217775e-17 0 1.7054560140922779 |
See Also
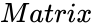 is the set of values.
is the set of values. ,
,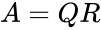 ,where
,where  stands for orthogonal matrix and
stands for orthogonal matrix and 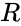 stands for Upper Triangular matrix.
stands for Upper Triangular matrix.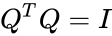 ,where
,where 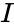 is identity or Unitary matrix.
is identity or Unitary matrix.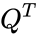 is the transpose matrix of Q.
is the transpose matrix of Q.