Difference between revisions of "Manuals/calci/SVF"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''SVF (Matrix)'''</div><br/> *<math>Matrix</math> is any set of values. ==Description== *This function shows the Singular value of a given matri...") |
|||
| Line 13: | Line 13: | ||
*To find Singular Value Decomposition we have to follow the below rules: | *To find Singular Value Decomposition we have to follow the below rules: | ||
*The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗. | *The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗. | ||
| − | *The right-singular vectors of M are a set of orthonormal eigenvectors of <math>M^ | + | *The right-singular vectors of M are a set of orthonormal eigenvectors of <math>M^{∗}M</math>. |
*The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both <math>M^∗M</math> and <math>MM^∗</math>. | *The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both <math>M^∗M</math> and <math>MM^∗</math>. | ||
Revision as of 16:11, 26 July 2017
SVF (Matrix)
- is any set of values.
Description
- This function shows the Singular value of a given matrix in descending order.
- In , is any matrix with array of values.
- Singular value decomposition is defined by the factorization of a real or complex matrix.
- It is the generalization of the Eigen decomposition of a symmetric matrix with positive eigen values to any mxn matrix through an extension of the polar decomposition.
- Singular value decomposition is of the form where is any square real or complex Unitary matrix of order .
- is a mxn rectangular diagonal matrix with non negative real numbers.
- V is also any square real or complex Unitary matrix of order nxn.
- The columns of U and V are called left Singular and right Singular vectors of the matrix.
- To find Singular Value Decomposition we have to follow the below rules:
*The left-singular vectors of the matrix M are a set of orthonormal eigenvectors of MM∗.
*The right-singular vectors of M are a set of orthonormal eigenvectors of Failed to parse (syntax error): {\displaystyle M^{∗}M}
.
*The non-zero singular values of M (found on the diagonal entries of Σ) are the square roots of the non-zero eigenvalues of both Failed to parse (syntax error): {\displaystyle M^∗M}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle MM^∗}
.
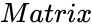 is any set of values.
is any set of values.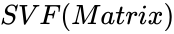 ,
, 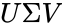 where
where 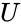 is any square real or complex Unitary matrix of order
is any square real or complex Unitary matrix of order 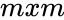 .
.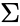 is a mxn rectangular diagonal matrix with non negative real numbers.
is a mxn rectangular diagonal matrix with non negative real numbers.