Difference between revisions of "Manuals/calci/ARGS"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''ARGS (Arguments)'''</div><br/> *<math>Arguments</math> is any complex number. ==Description== *This function is showing the arguments of a comp...") |
|||
| Line 5: | Line 5: | ||
*This function is showing the arguments of a complex numbers. | *This function is showing the arguments of a complex numbers. | ||
*In <math>ARGS (Arguments)</math>,<math>Arguments</math> is any complex number. | *In <math>ARGS (Arguments)</math>,<math>Arguments</math> is any complex number. | ||
| − | *A complex number z is represented by <math>z=x+iy=|z|e^{i \theta}. | + | *A complex number z is represented by <math>z=x+iy=|z|e^{i \theta}</math>. |
| − | *where <math>|z|</math> is a positive real number called the complex modulus of z, and theta | + | *where <math>|z|</math> is a positive real number called the complex modulus of z, and <math>\theta</math> is a real number called the argument. |
*The argument is sometimes also known as the phase or amplitude. | *The argument is sometimes also known as the phase or amplitude. | ||
*i.e The angle from the positive axis to the line segment is called the Argument of a complex number. | *i.e The angle from the positive axis to the line segment is called the Argument of a complex number. | ||
| Line 12: | Line 12: | ||
*The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta</math> in Radians. | *The argument of a complex number is calculated by <math>arg(z)= tan^{-1}(\frac{y}{x}) =\theta</math> in Radians. | ||
*Here it is showing all the arguments values are showing separately like real and imaginary values. | *Here it is showing all the arguments values are showing separately like real and imaginary values. | ||
| + | |||
| + | ==Examples== | ||
| + | 1.ARGS("2+3i") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 2 || + || 3 || i | ||
| + | |} | ||
| + | 2.ARGS("8-10i") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 8 || - || 1 || 0 || i | ||
| + | |} | ||
| + | 3.ARGS("45") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | 4 || 5 | ||
| + | |} | ||
| + | 4. ARGS("-56i") | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | - || 5 || 6 ||i | ||
| + | |} | ||
Revision as of 15:38, 2 August 2017
ARGS (Arguments)
- is any complex number.
Description
- This function is showing the arguments of a complex numbers.
- In , is any complex number.
- A complex number z is represented by .
- where is a positive real number called the complex modulus of z, and is a real number called the argument.
- The argument is sometimes also known as the phase or amplitude.
- i.e The angle from the positive axis to the line segment is called the Argument of a complex number.
- So x and y are any real numbers and i is the imaginary value,.
- The argument of a complex number is calculated by in Radians.
- Here it is showing all the arguments values are showing separately like real and imaginary values.
Examples
1.ARGS("2+3i")
| 2 | + | 3 | i |
2.ARGS("8-10i")
| 8 | - | 1 | 0 | i |
3.ARGS("45")
| 4 | 5 |
4. ARGS("-56i")
| - | 5 | 6 | i |
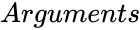 is any complex number.
is any complex number. ,
,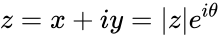 .
.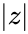 is a positive real number called the complex modulus of z, and
is a positive real number called the complex modulus of z, and 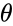 is a real number called the argument.
is a real number called the argument.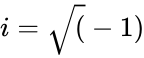 .
. in Radians.
in Radians.