Difference between revisions of "Manuals/calci/SVD"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
==Description== | ==Description== | ||
| − | *The singular value decomposition of a matrix A is the factorization of A into the product of three matrices <math>A = | + | *The singular value decomposition of a matrix A is the factorization of A into the product of three matrices <math>A = USV^T</math> |
| + | *Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries | ||
| + | *Singular value decomposition is defined for all matrices (rectangular or square). | ||
| + | |||
| + | Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers. | ||
| + | *Then there exists a factorization, called a singular value decomposition of A, of the form | ||
| + | |||
| + | where | ||
| + | |||
| + | U is an m × m unitary matrix, | ||
| + | S is a diagonal m × n matrix with non-negative real numbers on the diagonal, | ||
| + | V is an n × n unitary matrix over K, and | ||
| + | <math>V^T</math> is the conjugate transpose of V. | ||
Revision as of 08:46, 4 September 2017
SVD(Matrix)
- is the set of values.
is the set of values.Description
- The singular value decomposition of a matrix A is the factorization of A into the product of three matrices
- Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries
- Singular value decomposition is defined for all matrices (rectangular or square).
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers.
- Then there exists a factorization, called a singular value decomposition of A, of the form
where
U is an m × m unitary matrix, S is a diagonal m × n matrix with non-negative real numbers on the diagonal, V is an n × n unitary matrix over K, and is the conjugate transpose of V.
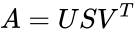
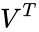is the conjugate transpose of V.