Difference between revisions of "Manuals/calci/SVD"
Jump to navigation
Jump to search
| Line 29: | Line 29: | ||
|- | |- | ||
! 2 | ! 2 | ||
| − | |-1 || -2 || 0 | + | | -1 || -2 || 0 |
|- | |- | ||
! 3 | ! 3 | ||
|0 || 1 || -1 | |0 || 1 || -1 | ||
|} | |} | ||
Revision as of 02:22, 5 September 2017
SVD(Matrix)
- is the set of values.
Description
- The singular value decomposition of a matrix A is the factorization of A into the product of three matrices
- Where the columns of U and V are orthonormal and the matrix S is diagonal with positive real entries
- Singular value decomposition is defined for all matrices (rectangular or square).
- The rank of a matrix is equal to the number of non-zero singular values.
Suppose A is a m × n matrix whose entries come from the field K, which is either the field of real numbers or the field of complex numbers.
- Then there exists a factorization, called a singular value decomposition of A, of the form
where U is an m × m unitary matrix, S is a diagonal m × n matrix with non-negative real numbers on the diagonal, V is an n × n unitary matrix over K, and is the conjugate transpose of V.
Example
| A | B | C | |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 2 | -1 | -2 | 0 |
| 3 | 0 | 1 | -1 |
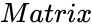 is the set of values.
is the set of values.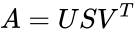
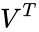 is the conjugate transpose of V.
is the conjugate transpose of V.