Difference between revisions of "Manuals/calci/DIAGONALWITH"
Jump to navigation
Jump to search
(Created page with "<div style="font-size:30px">'''DIAGONALWITH(Matrix,Properties,Seed,Offset,FillTypeAntiColumnOrRow)'''</div><br/> *<math>Matrix</math> is any nxn square matrix. ==Description...") |
|||
| Line 5: | Line 5: | ||
==Description== | ==Description== | ||
*This function gives the matrix satisfying the diagonal properties. | *This function gives the matrix satisfying the diagonal properties. | ||
| − | *An diagonal matrix is a matrix where all the entries are zero on the main diagonal going from the upper left corner to the lower right corner (<math>\ | + | *An diagonal matrix is a matrix where all the entries are zero on the main diagonal going from the upper left corner to the lower right corner (<math>\searrow</math>). |
*In Diagonalwith, all the elements on main diagonal are filled with the given Properties rather than by 0. | *In Diagonalwith, all the elements on main diagonal are filled with the given Properties rather than by 0. | ||
*A diagonal matrix is a square matrix which is of the form <math>a_{ij}=c_{i} \delta_{ij}</math> where <math>\delta_{ij}</math> is the Kronecker delta, <math>c_{i}</math> are constants, and i,j=1, 2, ..., n. | *A diagonal matrix is a square matrix which is of the form <math>a_{ij}=c_{i} \delta_{ij}</math> where <math>\delta_{ij}</math> is the Kronecker delta, <math>c_{i}</math> are constants, and i,j=1, 2, ..., n. | ||
Revision as of 08:51, 10 January 2018
DIAGONALWITH(Matrix,Properties,Seed,Offset,FillTypeAntiColumnOrRow)
- is any nxn square matrix.
Description
- This function gives the matrix satisfying the diagonal properties.
- An diagonal matrix is a matrix where all the entries are zero on the main diagonal going from the upper left corner to the lower right corner ().
- In Diagonalwith, all the elements on main diagonal are filled with the given Properties rather than by 0.
- A diagonal matrix is a square matrix which is of the form where is the Kronecker delta, are constants, and i,j=1, 2, ..., n.
- The general diagonal matrix is of the form:
- So the main diagonal entries are need not to be zero and off-diagonal entries are zero.
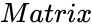 is any nxn square matrix.
is any nxn square matrix.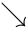 ).
).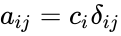 where
where 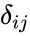 is the Kronecker delta,
is the Kronecker delta, 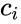 are constants, and i,j=1, 2, ..., n.
are constants, and i,j=1, 2, ..., n.